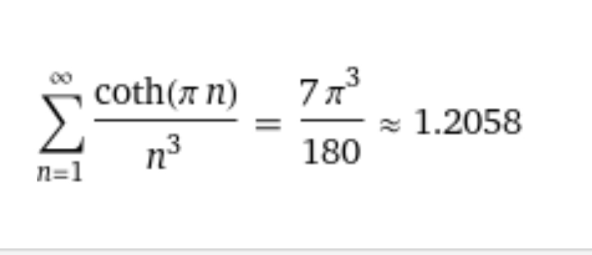Question Number 131686 by Dwaipayan Shikari last updated on 07/Feb/21

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left({n}\pi\right)}{{n}^{\mathrm{3}} } \\ $$
Commented by Dwaipayan Shikari last updated on 07/Feb/21
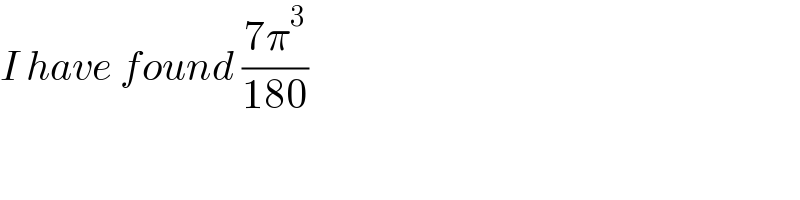
$${I}\:{have}\:{found}\:\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{180}} \\ $$
Commented by Dwaipayan Shikari last updated on 07/Feb/21
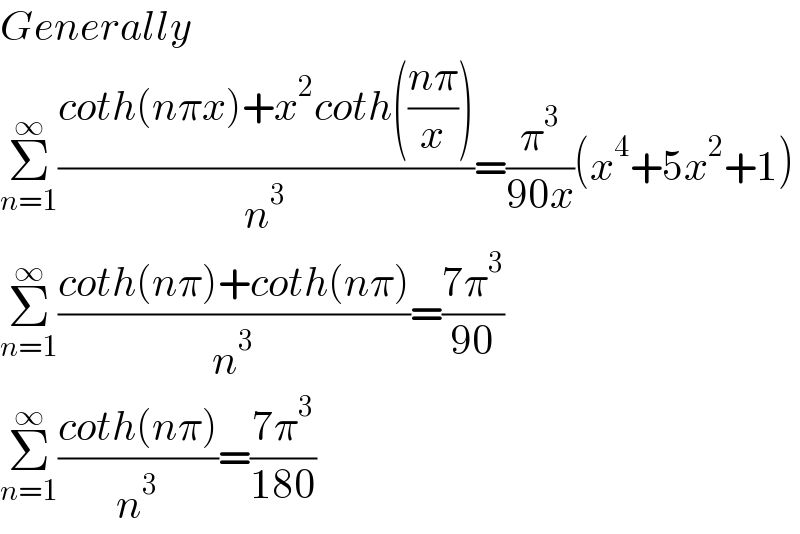
$${Generally} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left({n}\pi{x}\right)+{x}^{\mathrm{2}} {coth}\left(\frac{{n}\pi}{{x}}\right)}{{n}^{\mathrm{3}} }=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}\left({x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left({n}\pi\right)+{coth}\left({n}\pi\right)}{{n}^{\mathrm{3}} }=\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{90}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left({n}\pi\right)}{{n}^{\mathrm{3}} }=\frac{\mathrm{7}\pi^{\mathrm{3}} }{\mathrm{180}} \\ $$
Commented by mnjuly1970 last updated on 07/Feb/21
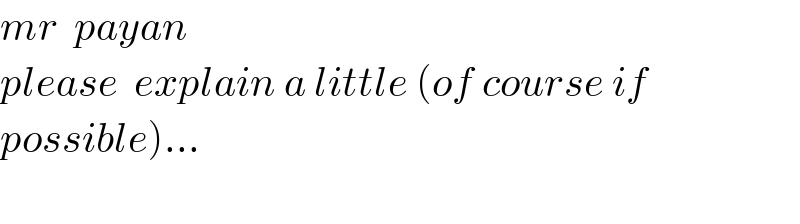
$${mr}\:\:{payan}\: \\ $$$${please}\:\:{explain}\:{a}\:{little}\:\left({of}\:{course}\:{if}\right. \\ $$$$\left.{possible}\right)… \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 07/Feb/21
![coth(πx)=(1/(πx))+((2x)/π)Σ_(k=1) ^∞ (1/(k^2 +x^2 )) [from ((sinh(πx))/(πx)) =Π_(n=1) ^∞ (1+(x^2 /n^2 ))] coth(πnx)=(1/(πnx))+((2xn)/π)Σ_(k=1) ^∞ (1/(k^2 +n^2 x^2 )) Σ_(n=1) ^∞ ((coth(πnx)+x^2 coth(((πn)/x)))/n^3 ) =Σ_(n=1) ^∞ (1/(πn^4 x))+((2x)/π)Σ_n Σ_k (1/n^2 ).(1/((k^2 +n^2 x^2 )))+Σ_n (x^3 /(πn^4 ))+((2x^3 )/π)Σ_n Σ_k (1/(n^2 (k^2 x^2 +n^2 ))) =(π^3 /(90x))+((π^3 x^3 )/(90))+((2x)/π)Σ_n Σ_k (1/(n^2 (k^2 +n^2 x^2 )))+((2x^3 )/π)Σ_n Σ_k (1/(n^2 (k^2 x^2 +n^2 ))) =(π^3 /(90x))(x^4 +1)+((2x)/π)(Σ_n Σ_k (k^2 /(n^2 k^2 (k^2 +n^2 x^2 )))+Σ_n Σ_k ((x^2 k^2 )/(n^2 k^2 (k^2 x^2 +n^2 )))) =(π^3 /(90x))(x^4 +1)+((2x)/π)(Σ_n Σ_k (1/(n^2 k^2 ))) =(π^3 /(90x))(x^4 +1)+((π^3 x)/(18))=(π^3 /(90x))(x^4 +5x^2 +1)](https://www.tinkutara.com/question/Q131720.png)
$${coth}\left(\pi{x}\right)=\frac{\mathrm{1}}{\pi{x}}+\frac{\mathrm{2}{x}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{from}\:\:\frac{{sinh}\left(\pi{x}\right)}{\pi{x}}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right] \\ $$$${coth}\left(\pi{nx}\right)=\frac{\mathrm{1}}{\pi{nx}}+\frac{\mathrm{2}{xn}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{coth}\left(\pi{nx}\right)+{x}^{\mathrm{2}} {coth}\left(\frac{\pi{n}}{{x}}\right)}{{n}^{\mathrm{3}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi{n}^{\mathrm{4}} {x}}+\frac{\mathrm{2}{x}}{\pi}\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\frac{\mathrm{1}}{\left({k}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}+\underset{{n}} {\sum}\frac{{x}^{\mathrm{3}} }{\pi{n}^{\mathrm{4}} }+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\pi}\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({k}^{\mathrm{2}} {x}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}+\frac{\pi^{\mathrm{3}} {x}^{\mathrm{3}} }{\mathrm{90}}+\frac{\mathrm{2}{x}}{\pi}\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({k}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\pi}\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({k}^{\mathrm{2}} {x}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}\left({x}^{\mathrm{4}} +\mathrm{1}\right)+\frac{\mathrm{2}{x}}{\pi}\left(\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} {k}^{\mathrm{2}} \left({k}^{\mathrm{2}} +{n}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}+\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{{x}^{\mathrm{2}} {k}^{\mathrm{2}} }{{n}^{\mathrm{2}} {k}^{\mathrm{2}} \left({k}^{\mathrm{2}} {x}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)}\right) \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}\left({x}^{\mathrm{4}} +\mathrm{1}\right)+\frac{\mathrm{2}{x}}{\pi}\left(\underset{{n}} {\sum}\underset{{k}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} {k}^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}\left({x}^{\mathrm{4}} +\mathrm{1}\right)+\frac{\pi^{\mathrm{3}} {x}}{\mathrm{18}}=\frac{\pi^{\mathrm{3}} }{\mathrm{90}{x}}\left({x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}\right)\: \\ $$
Commented by mnjuly1970 last updated on 07/Feb/21
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{payan}.. \\ $$$$\:{grateful}… \\ $$
Commented by mnjuly1970 last updated on 07/Feb/21
$${excellent}.{bravo}…{bravo}… \\ $$$${very}\:{nice}.. \\ $$
Answered by rs4089 last updated on 07/Feb/21