Menu Close

n-1-n-2-1-n-2-n-1-4n-2-4n-2-4n-2-4n-1-

Tinku Tara 0 Comments
Pin




Question Number 133628 by Ñï= last updated on 23/Feb/21
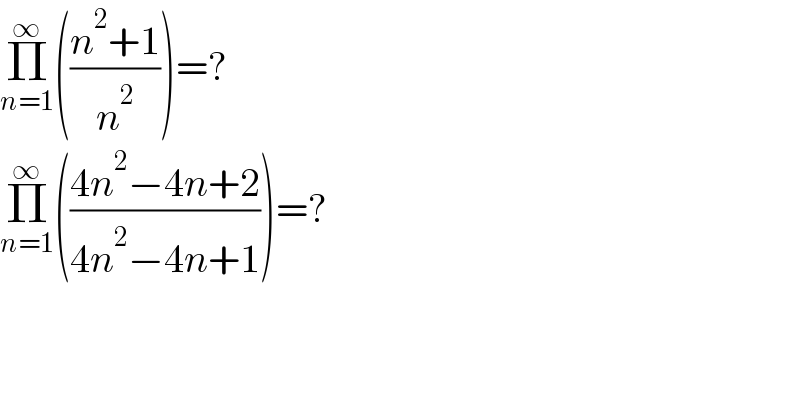
Π_(n=1) ^∞ (((n^2 +1)/n^2 ))=? Π_(n=1) ^∞ (((4n^2 −4n+2)/(4n^2 −4n+1)))=?
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{{n}^{\mathrm{2}} +\mathrm{1}}{{n}^{\mathrm{2}} }\right)=? \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{2}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{1}}\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 23/Feb/21
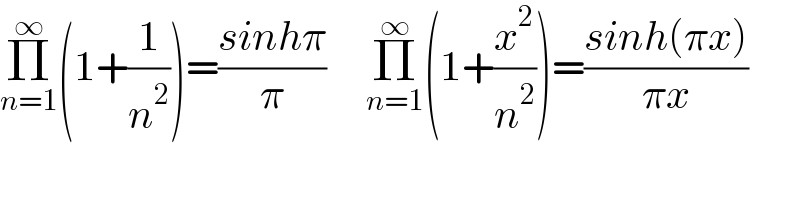
Π_(n=1) ^∞ (1+(1/n^2 ))=((sinhπ)/π) Π_(n=1) ^∞ (1+(x^2 /n^2 ))=((sinh(πx))/(πx))
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\frac{{sinh}\pi}{\pi}\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)=\frac{{sinh}\left(\pi{x}\right)}{\pi{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Feb/21
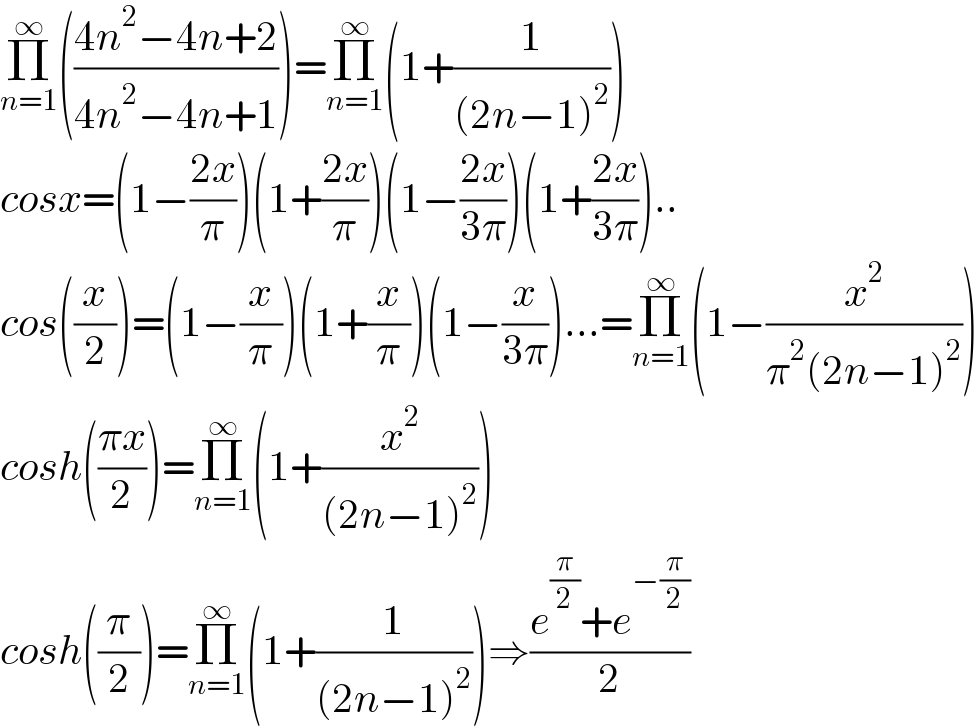
Π_(n=1) ^∞ (((4n^2 −4n+2)/(4n^2 −4n+1)))=Π_(n=1) ^∞ (1+(1/((2n−1)^2 ))) cosx=(1−((2x)/π))(1+((2x)/π))(1−((2x)/(3π)))(1+((2x)/(3π))).. cos((x/2))=(1−(x/π))(1+(x/π))(1−(x/(3π)))...=Π_(n=1) ^∞ (1−(x^2 /(π^2 (2n−1)^2 ))) cosh(((πx)/2))=Π_(n=1) ^∞ (1+(x^2 /((2n−1)^2 ))) cosh((π/2))=Π_(n=1) ^∞ (1+(1/((2n−1)^2 )))⇒((e^(π/2) +e^(−(π/2)) )/2)
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{2}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{1}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$${cosx}=\left(\mathrm{1}−\frac{\mathrm{2}{x}}{\pi}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\pi}\right)\left(\mathrm{1}−\frac{\mathrm{2}{x}}{\mathrm{3}\pi}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{3}\pi}\right).. \\ $$$${cos}\left(\frac{{x}}{\mathrm{2}}\right)=\left(\mathrm{1}−\frac{{x}}{\pi}\right)\left(\mathrm{1}+\frac{{x}}{\pi}\right)\left(\mathrm{1}−\frac{{x}}{\mathrm{3}\pi}\right)…=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} \left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$${cosh}\left(\frac{\pi{x}}{\mathrm{2}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$${cosh}\left(\frac{\pi}{\mathrm{2}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right)\Rightarrow\frac{{e}^{\frac{\pi}{\mathrm{2}}} +{e}^{−\frac{\pi}{\mathrm{2}}} }{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *