Question Number 78460 by Tony Lin last updated on 17/Jan/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}^{\mathrm{3}} }{\mathrm{3}^{{n}} }=? \\ $$
Commented by mathmax by abdo last updated on 18/Jan/20

$${let}\:{s}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}^{\mathrm{3}} }{\mathrm{3}^{{n}} }\:\:{and}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} {x}^{{n}} \:\:{with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow{f}^{\left(\mathrm{1}\right)} \left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} {nx}^{{n}−\mathrm{1}} \:\Rightarrow\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} =\left(\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right)^{\left(\mathrm{1}\right)} =\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{1}\right){x}}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{{x}−\mathrm{1}−\mathrm{2}{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }\:=\frac{−{x}−\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }\:=\frac{{x}+\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} {x}^{{n}} \:=\frac{{x}^{\mathrm{2}} +{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} {n}^{\mathrm{3}} {x}^{{n}−\mathrm{1}} =\left(\frac{{x}^{\mathrm{2}} +{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\right)^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{1}−{x}\right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{6}} }\:=\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{1}−{x}\right)+\mathrm{3}\left({x}^{\mathrm{2}} +{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−{x}\:+\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{3}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:=\frac{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} {n}^{\mathrm{3}} {x}^{{n}} =\frac{{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$$\Rightarrow{s}\:={f}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} \:+\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{3}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{4}} }\:=\frac{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{2}^{\mathrm{4}} }{\mathrm{3}^{\mathrm{4}} }} \\ $$$$=\frac{\mathrm{3}^{\mathrm{4}} \left\{\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\right\}}{\mathrm{16}}\:=\frac{\mathrm{3}+\mathrm{36}\:+\mathrm{27}}{\mathrm{16}}\:=\frac{\mathrm{39}+\mathrm{27}}{\mathrm{16}}\:=\frac{\mathrm{66}}{\mathrm{16}}\:=\frac{\mathrm{33}}{\mathrm{8}} \\ $$$$\bigstar\:{s}=\frac{\mathrm{33}}{\mathrm{8}}\bigstar \\ $$
Commented by Tony Lin last updated on 18/Jan/20

$${thanks}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 18/Jan/20

$${you}\:{are}\:{welcome} \\ $$
Answered by mr W last updated on 17/Jan/20

$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +…=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{4}} +…=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{2}} {x}+\mathrm{3}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{3}} +…=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${x}+\mathrm{2}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} {x}^{\mathrm{3}} +\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{4}} +…=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{3}} {x}+\mathrm{3}^{\mathrm{3}} {x}^{\mathrm{2}} +\mathrm{4}^{\mathrm{3}} {x}^{\mathrm{3}} +…=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$${x}+\mathrm{2}^{\mathrm{3}} {x}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} {x}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} {x}^{\mathrm{4}} +…=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$${let}\:{x}=\frac{\mathrm{1}}{\mathrm{3}}: \\ $$$$\frac{\mathrm{1}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{4}} }+…=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{3}} }{\mathrm{3}^{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{6}}{\mathrm{3}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{6}}{\mathrm{3}^{\mathrm{3}} }×\frac{\mathrm{3}^{\mathrm{4}} }{\mathrm{2}^{\mathrm{4}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{3}} }{\mathrm{3}^{{n}} }=\frac{\mathrm{33}}{\mathrm{8}} \\ $$
Commented by Tony Lin last updated on 18/Jan/20

$${thanks}\:{sir} \\ $$
Answered by mind is power last updated on 17/Jan/20
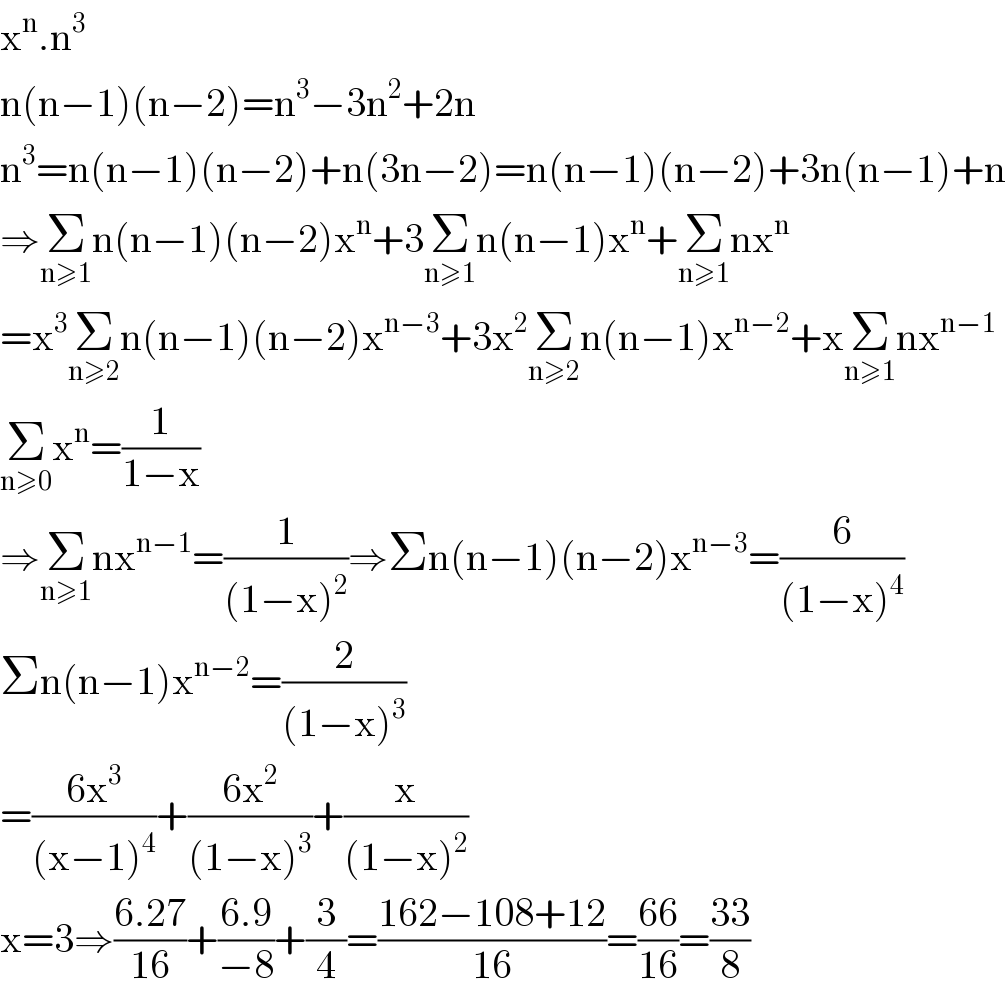
$$\mathrm{x}^{\mathrm{n}} .\mathrm{n}^{\mathrm{3}} \\ $$$$\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)=\mathrm{n}^{\mathrm{3}} −\mathrm{3n}^{\mathrm{2}} +\mathrm{2n} \\ $$$$\mathrm{n}^{\mathrm{3}} =\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)+\mathrm{n}\left(\mathrm{3n}−\mathrm{2}\right)=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)+\mathrm{3n}\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{n} \\ $$$$\Rightarrow\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\mathrm{x}^{\mathrm{n}} +\mathrm{3}\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} +\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{nx}^{\mathrm{n}} \\ $$$$=\mathrm{x}^{\mathrm{3}} \underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\mathrm{x}^{\mathrm{n}−\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} \underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} +\mathrm{x}\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \\ $$$$\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\mathrm{x}^{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$\Rightarrow\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{nx}^{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\Rightarrow\Sigma\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\mathrm{x}^{\mathrm{n}−\mathrm{3}} =\frac{\mathrm{6}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{4}} } \\ $$$$\Sigma\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} =\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{6x}^{\mathrm{3}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{6x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }+\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}=\mathrm{3}\Rightarrow\frac{\mathrm{6}.\mathrm{27}}{\mathrm{16}}+\frac{\mathrm{6}.\mathrm{9}}{−\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{162}−\mathrm{108}+\mathrm{12}}{\mathrm{16}}=\frac{\mathrm{66}}{\mathrm{16}}=\frac{\mathrm{33}}{\mathrm{8}} \\ $$
Commented by Tony Lin last updated on 18/Jan/20

$${thanks}\:{sir} \\ $$
Commented by mind is power last updated on 18/Jan/20

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
Answered by john santu last updated on 18/Jan/20

$${let}\:{S}=\:\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{9}}+\frac{\mathrm{27}}{\mathrm{27}}+\frac{\mathrm{64}}{\mathrm{81}}+\frac{\mathrm{125}}{\mathrm{243}}+…\:\left(\mathrm{1}\right) \\ $$$${by}\:{multiply}\:{in}\:{both}\:{side}\:{with}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{S}=\:\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{8}}{\mathrm{27}}+\frac{\mathrm{27}}{\mathrm{64}}+\frac{\mathrm{64}}{\mathrm{243}}+…\:\left(\mathrm{2}\right) \\ $$$${substract}\:{equations}\:\mathrm{1}\:{and}\:\mathrm{2} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{S}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{9}}+\frac{\mathrm{19}}{\mathrm{27}}+\frac{\mathrm{37}}{\mathrm{81}}+\frac{\mathrm{61}}{\mathrm{243}}+…\left(\mathrm{3}\right) \\ $$$$\frac{\mathrm{2}}{\mathrm{9}}{S}=\:\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{7}}{\mathrm{27}}+\frac{\mathrm{19}}{\mathrm{81}}+\frac{\mathrm{37}}{\mathrm{243}}+… \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}{S}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{9}}+\frac{\mathrm{12}}{\mathrm{27}}+\frac{\mathrm{18}}{\mathrm{81}}+\frac{\mathrm{24}}{\mathrm{243}}+… \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}{S}=\:\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{27}}+\frac{\mathrm{3}}{\mathrm{81}}+\frac{\mathrm{4}}{\mathrm{243}}+…\right) \\ $$$${let}\:{P}=\:\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{27}}+\frac{\mathrm{3}}{\mathrm{81}}+\frac{\mathrm{4}}{\mathrm{243}}+… \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{P}=\:\frac{\mathrm{1}}{\mathrm{27}}+\frac{\mathrm{2}}{\mathrm{81}}+\frac{\mathrm{3}}{\mathrm{243}}+… \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{P}=\:\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{27}}+\frac{\mathrm{1}}{\mathrm{81}}+\frac{\mathrm{1}}{\mathrm{243}}+…=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{P}=\:\frac{\mathrm{1}}{\mathrm{4}}\:.\:{now}\:{we}\:{get}\: \\ $$$$\frac{\mathrm{4}}{\mathrm{9}}{S}=\:\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{6}×\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{S}=\:\frac{\mathrm{33}}{\mathrm{8}\:}\:.\bigstar \\ $$
Commented by Tony Lin last updated on 18/Jan/20

$${thanks}\:{sir} \\ $$
