Question Number 141811 by mnjuly1970 last updated on 23/May/21
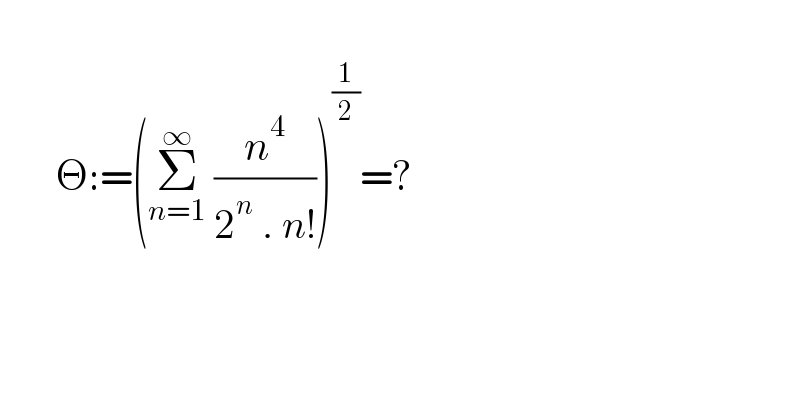
$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\Theta:=\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}^{\mathrm{4}} }{\mathrm{2}^{{n}} \:.\:{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =? \\ $$
Answered by qaz last updated on 23/May/21
![(xD)^4 =xDxDxDxD =xDxDx(D+xD^2 ) =xDx[(D+xD^2 )+x(D^2 +D^2 +xD^3 ] =xDx(D+3xD^2 +x^2 D^3 ) =x[(D+3xD^2 +x^2 D^3 )+x(D^2 +3D^2 +3xD^3 +2xD^3 +x^2 D^4 )] =xD+7x^2 D^2 +6x^3 D^3 +x^4 D^4 Θ=(Σ_(n=1) ^∞ (n^4 /(2^n n!)))^2 =((xD)^4 (Σ_(n=0) ^∞ (x^n /(n!))−1))^(1/2) ∣_(x=1/2) =[(xD)^4 (e^x −1)]^(1/2) ∣_(x=1/2) =[(x+7x^2 +6x^3 +x^4 )e^x ]^(1/2) ∣_(x=1/2) =((1/2)+(7/4)+(6/8)+(1/(16)))^(1/2) (e)^(1/4) =(7/4)(e)^(1/4)](https://www.tinkutara.com/question/Q141837.png)
$$\left({xD}\right)^{\mathrm{4}} \\ $$$$={xDxDxDxD} \\ $$$$={xDxDx}\left({D}+{xD}^{\mathrm{2}} \right) \\ $$$$={xDx}\left[\left({D}+{xD}^{\mathrm{2}} \right)+{x}\left({D}^{\mathrm{2}} +{D}^{\mathrm{2}} +{xD}^{\mathrm{3}} \right]\right. \\ $$$$={xDx}\left({D}+\mathrm{3}{xD}^{\mathrm{2}} +{x}^{\mathrm{2}} {D}^{\mathrm{3}} \right) \\ $$$$={x}\left[\left({D}+\mathrm{3}{xD}^{\mathrm{2}} +{x}^{\mathrm{2}} {D}^{\mathrm{3}} \right)+{x}\left({D}^{\mathrm{2}} +\mathrm{3}{D}^{\mathrm{2}} +\mathrm{3}{xD}^{\mathrm{3}} +\mathrm{2}{xD}^{\mathrm{3}} +{x}^{\mathrm{2}} {D}^{\mathrm{4}} \right)\right] \\ $$$$={xD}+\mathrm{7}{x}^{\mathrm{2}} {D}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{3}} {D}^{\mathrm{3}} +{x}^{\mathrm{4}} {D}^{\mathrm{4}} \\ $$$$\Theta=\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{4}} }{\mathrm{2}^{{n}} {n}!}\right)^{\mathrm{2}} =\left(\left({xD}\right)^{\mathrm{4}} \left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}−\mathrm{1}\right)\right)^{\mathrm{1}/\mathrm{2}} \mid_{{x}=\mathrm{1}/\mathrm{2}} \\ $$$$=\left[\left({xD}\right)^{\mathrm{4}} \left({e}^{{x}} −\mathrm{1}\right)\right]^{\mathrm{1}/\mathrm{2}} \mid_{{x}=\mathrm{1}/\mathrm{2}} \\ $$$$=\left[\left({x}+\mathrm{7}{x}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right){e}^{{x}} \right]^{\mathrm{1}/\mathrm{2}} \mid_{{x}=\mathrm{1}/\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{4}}+\frac{\mathrm{6}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{16}}\right)^{\mathrm{1}/\mathrm{2}} \sqrt[{\mathrm{4}}]{{e}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{4}}\sqrt[{\mathrm{4}}]{{e}} \\ $$
Commented by mnjuly1970 last updated on 23/May/21
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{qaz}.. \\ $$
