Question Number 133264 by Dwaipayan Shikari last updated on 20/Feb/21

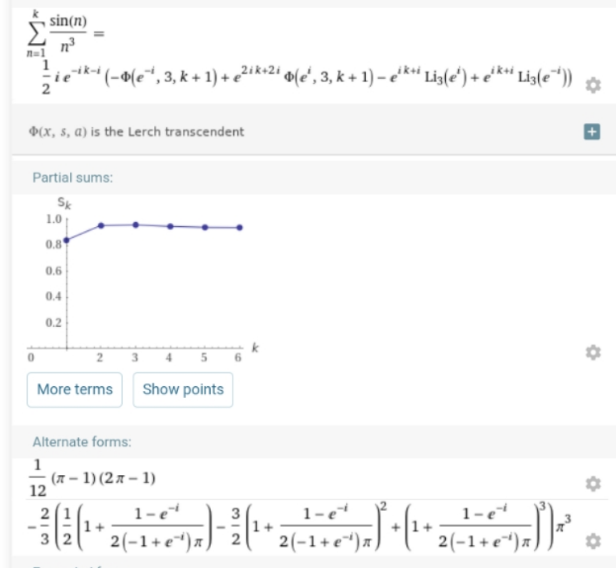
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sinn}}{{n}^{\mathrm{3}} } \\ $$
Commented by Dwaipayan Shikari last updated on 20/Feb/21
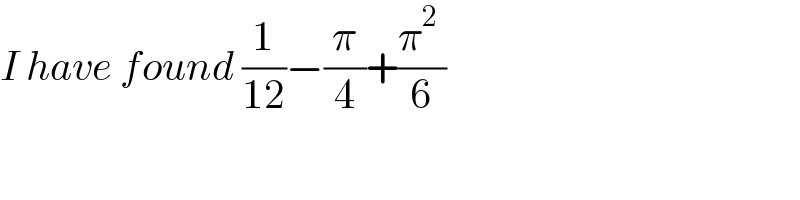
$${I}\:{have}\:{found}\:\frac{\mathrm{1}}{\mathrm{12}}−\frac{\pi}{\mathrm{4}}+\frac{\pi^{\mathrm{2}} \:}{\mathrm{6}} \\ $$
Answered by mnjuly1970 last updated on 20/Feb/21
![properties of trilogarithm.. li_3 (z)−li_3 ((1/z))=−(1/6)ln^3 (−z)−(1/6)π^2 ln(−z) (1/(2i))(Σ_(n=1) ^∞ (e^(in) /n^3 )−(e^(−in) /n^3 ))=(1/(2i))(li_3 (e^i )−li_3 ((1/e^i ))) =(i/(12))(ln^3 (−e^i )+π^2 ln(−e^i )) =(i/(12))ln(i^2 e^i )((ln(i^2 )+ln(e^i ))^2 +π^2 ) =(i/(12))(2ln(i)+i)[(2ln(i)+i)^2 +π^2 ] =(i/(12))(i)(π+1)[−(π+1)^2 +π^2 ] =−((π+1)/(12))(−2π−1) =(π^2 /6)+(π/4)+(1/(12)) =....](https://www.tinkutara.com/question/Q133273.png)
$$\:{properties}\:{of}\:{trilogarithm}.. \\ $$$$\:\:{li}_{\mathrm{3}} \left({z}\right)−{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{{z}}\right)=−\frac{\mathrm{1}}{\mathrm{6}}{ln}^{\mathrm{3}} \left(−{z}\right)−\frac{\mathrm{1}}{\mathrm{6}}\pi^{\mathrm{2}} {ln}\left(−{z}\right) \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{in}} }{{n}^{\mathrm{3}} }−\frac{{e}^{−{in}} }{{n}^{\mathrm{3}} }\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left({li}_{\mathrm{3}} \left({e}^{{i}} \right)−{li}_{\mathrm{3}} \left(\frac{\mathrm{1}}{{e}^{{i}} }\right)\right) \\ $$$$=\frac{{i}}{\mathrm{12}}\left({ln}^{\mathrm{3}} \left(−{e}^{{i}} \right)+\pi^{\mathrm{2}} {ln}\left(−{e}^{{i}} \right)\right) \\ $$$$=\frac{{i}}{\mathrm{12}}{ln}\left({i}^{\mathrm{2}} {e}^{{i}} \right)\left(\left({ln}\left({i}^{\mathrm{2}} \right)+{ln}\left({e}^{{i}} \right)\right)^{\mathrm{2}} +\pi^{\mathrm{2}} \right) \\ $$$$=\frac{{i}}{\mathrm{12}}\left(\mathrm{2}{ln}\left({i}\right)+{i}\right)\left[\left(\mathrm{2}{ln}\left({i}\right)+{i}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} \right] \\ $$$$=\frac{{i}}{\mathrm{12}}\left({i}\right)\left(\pi+\mathrm{1}\right)\left[−\left(\pi+\mathrm{1}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} \right] \\ $$$$=−\frac{\pi+\mathrm{1}}{\mathrm{12}}\left(−\mathrm{2}\pi−\mathrm{1}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{12}}\:=…. \\ $$
Commented by Dwaipayan Shikari last updated on 20/Feb/21