Question Number 137721 by Ñï= last updated on 05/Apr/21
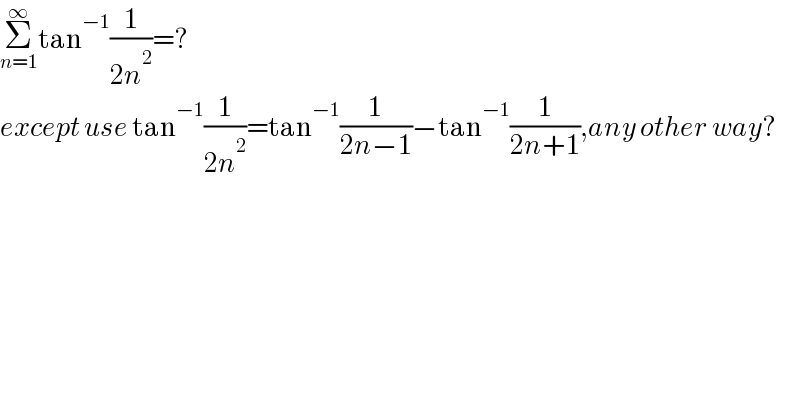
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }=? \\ $$$${except}\:{use}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}},{any}\:{other}\:{way}? \\ $$
Answered by TANMAY PANACEA last updated on 05/Apr/21
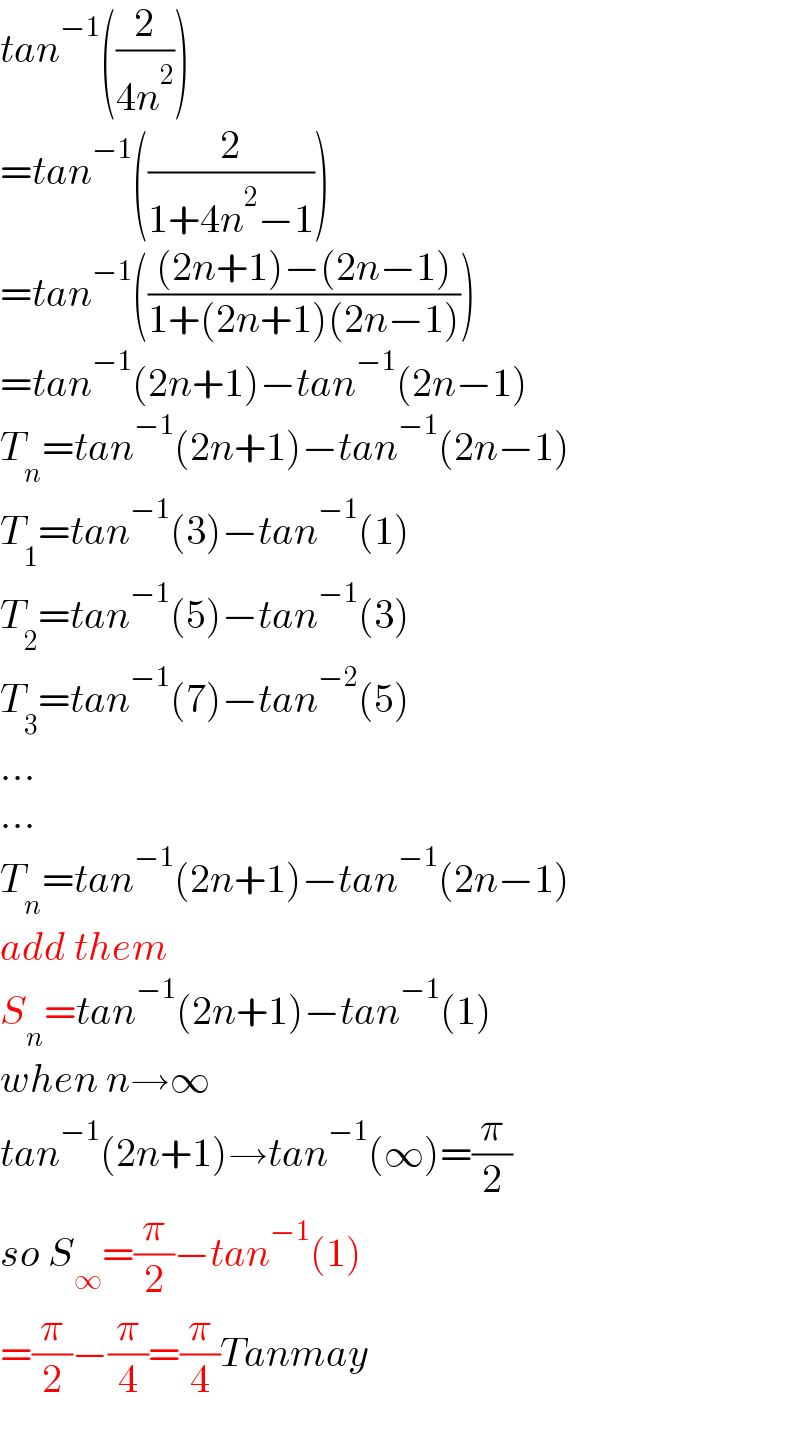
$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{4}{n}^{\mathrm{2}} }\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)−\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${T}_{{n}} ={tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${T}_{\mathrm{1}} ={tan}^{−\mathrm{1}} \left(\mathrm{3}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$${T}_{\mathrm{2}} ={tan}^{−\mathrm{1}} \left(\mathrm{5}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{3}\right) \\ $$$${T}_{\mathrm{3}} ={tan}^{−\mathrm{1}} \left(\mathrm{7}\right)−{tan}^{−\mathrm{2}} \left(\mathrm{5}\right) \\ $$$$… \\ $$$$… \\ $$$${T}_{{n}} ={tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${add}\:{them} \\ $$$${S}_{{n}} ={tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$${when}\:{n}\rightarrow\infty \\ $$$${tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)\rightarrow{tan}^{−\mathrm{1}} \left(\infty\right)=\frac{\pi}{\mathrm{2}} \\ $$$${so}\:{S}_{\infty} =\frac{\pi}{\mathrm{2}}−{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}}{Tanmay}\: \\ $$
Commented by Ñï= last updated on 06/Apr/21

$${thanks}\:{sir} \\ $$
Commented by TANMAY PANACEA last updated on 06/Apr/21

$${most}\:{welcome} \\ $$
