Question Number 12326 by sin (x) last updated on 19/Apr/17

$$\underset{{n}=\mathrm{1}} {\overset{{x}} {\prod}}{a}_{{n}} =\mathrm{9}^{{x}!} \\ $$$${a}_{\mathrm{4}} =? \\ $$
Answered by nume1114 last updated on 19/Apr/17
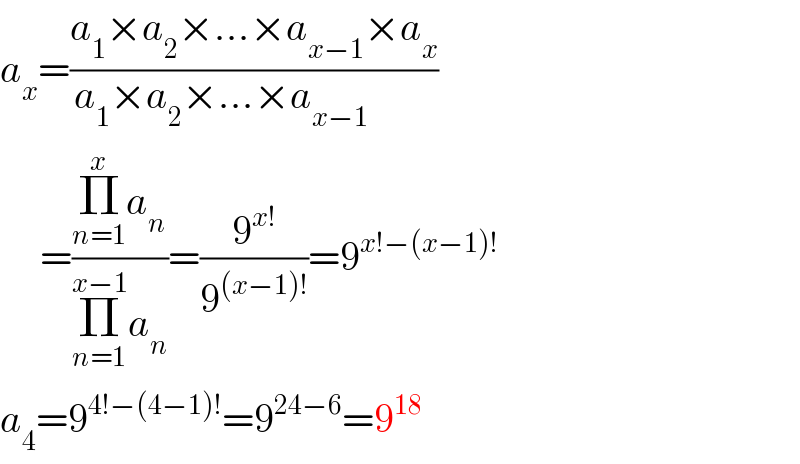
$${a}_{{x}} =\frac{{a}_{\mathrm{1}} ×{a}_{\mathrm{2}} ×…×{a}_{{x}−\mathrm{1}} ×{a}_{{x}} }{{a}_{\mathrm{1}} ×{a}_{\mathrm{2}} ×…×{a}_{{x}−\mathrm{1}} \:\:\:\:\:\:\:\:} \\ $$$$\:\:\:\:\:=\frac{\underset{{n}=\mathrm{1}} {\overset{{x}} {\prod}}{a}_{{n}} }{\underset{{n}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\prod}}{a}_{{n}} }=\frac{\mathrm{9}^{{x}!} }{\mathrm{9}^{\left({x}−\mathrm{1}\right)!} }=\mathrm{9}^{{x}!−\left({x}−\mathrm{1}\right)!} \\ $$$${a}_{\mathrm{4}} =\mathrm{9}^{\mathrm{4}!−\left(\mathrm{4}−\mathrm{1}\right)!} =\mathrm{9}^{\mathrm{24}−\mathrm{6}} =\mathrm{9}^{\mathrm{18}} \\ $$
