Question Number 6982 by FilupSmith last updated on 04/Aug/16

$${n}={p}^{{n}} −{pn} \\ $$$${n}=? \\ $$
Commented by sou1618 last updated on 05/Aug/16
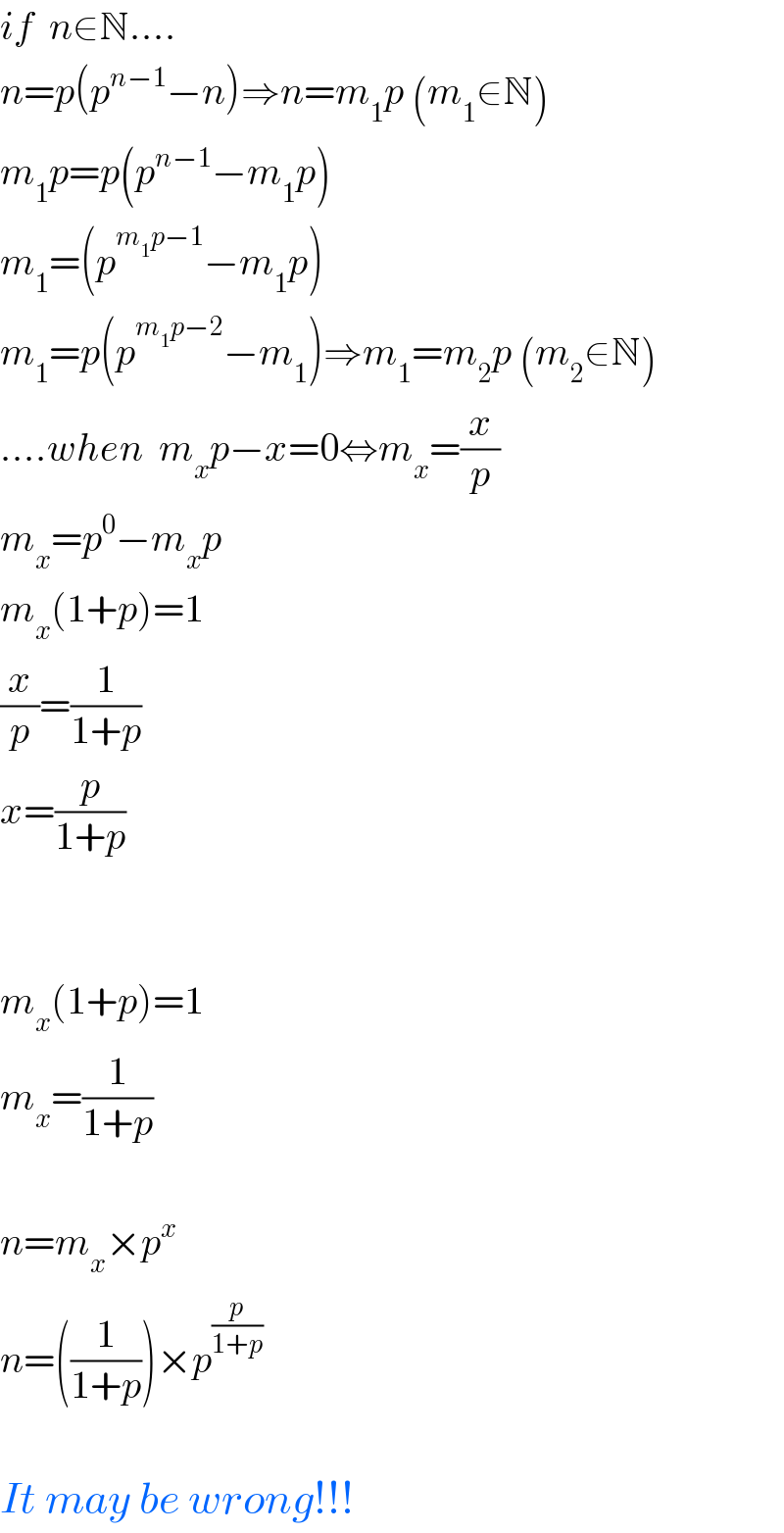
$${if}\:\:{n}\in\mathbb{N}…. \\ $$$${n}={p}\left({p}^{{n}−\mathrm{1}} −{n}\right)\Rightarrow{n}={m}_{\mathrm{1}} {p}\:\left({m}_{\mathrm{1}} \in\mathbb{N}\right) \\ $$$${m}_{\mathrm{1}} {p}={p}\left({p}^{{n}−\mathrm{1}} −{m}_{\mathrm{1}} {p}\right) \\ $$$${m}_{\mathrm{1}} =\left({p}^{{m}_{\mathrm{1}} {p}−\mathrm{1}} −{m}_{\mathrm{1}} {p}\right) \\ $$$${m}_{\mathrm{1}} ={p}\left({p}^{{m}_{\mathrm{1}} {p}−\mathrm{2}} −{m}_{\mathrm{1}} \right)\Rightarrow{m}_{\mathrm{1}} ={m}_{\mathrm{2}} {p}\:\left({m}_{\mathrm{2}} \in\mathbb{N}\right) \\ $$$$….{when}\:\:{m}_{{x}} {p}−{x}=\mathrm{0}\Leftrightarrow{m}_{{x}} =\frac{{x}}{{p}} \\ $$$${m}_{{x}} ={p}^{\mathrm{0}} −{m}_{{x}} {p} \\ $$$${m}_{{x}} \left(\mathrm{1}+{p}\right)=\mathrm{1} \\ $$$$\frac{{x}}{{p}}=\frac{\mathrm{1}}{\mathrm{1}+{p}} \\ $$$${x}=\frac{{p}}{\mathrm{1}+{p}} \\ $$$$ \\ $$$$ \\ $$$${m}_{{x}} \left(\mathrm{1}+{p}\right)=\mathrm{1} \\ $$$${m}_{{x}} =\frac{\mathrm{1}}{\mathrm{1}+{p}} \\ $$$$ \\ $$$${n}={m}_{{x}} ×{p}^{{x}} \\ $$$${n}=\left(\frac{\mathrm{1}}{\mathrm{1}+{p}}\right)×{p}^{\frac{{p}}{\mathrm{1}+{p}}} \\ $$$$ \\ $$$${It}\:{may}\:{be}\:{wrong}!!! \\ $$
Commented by Yozzii last updated on 05/Aug/16
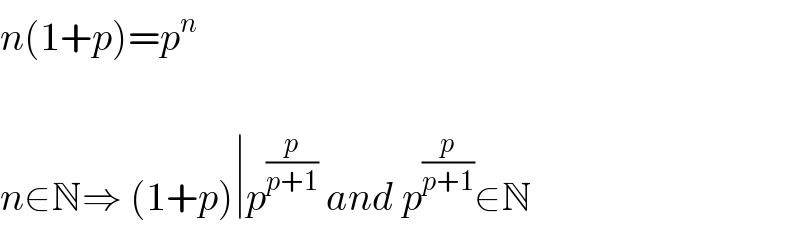
$${n}\left(\mathrm{1}+{p}\right)={p}^{{n}} \\ $$$$ \\ $$$${n}\in\mathbb{N}\Rightarrow\:\left(\mathrm{1}+{p}\right)\mid{p}^{\frac{{p}}{{p}+\mathrm{1}}} \:{and}\:{p}^{\frac{{p}}{{p}+\mathrm{1}}} \in\mathbb{N} \\ $$
Commented by sou1618 last updated on 05/Aug/16

$${oh}…\left(×\_×;\right) \\ $$
