Question Number 139561 by physicstutes last updated on 28/Apr/21

$$\mathrm{Near}\:\mathrm{the}\:\mathrm{shore}\:\mathrm{a}\:\mathrm{fisherman}\:\mathrm{jumps}\:\mathrm{out}\:\mathrm{of}\:\mathrm{his}\:\mathrm{boat}\:\mathrm{with}\:\mathrm{a}\:\mathrm{velocity} \\ $$$$\mathrm{of}\:\mathrm{5}.\mathrm{00}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{and}\:\mathrm{lands}\:\mathrm{on}\:\mathrm{the}\:\mathrm{shore}\:\mathrm{0}.\mathrm{650}\:\mathrm{afterwards}.\mathrm{The}\:\mathrm{boat} \\ $$$$\mathrm{moves}\:\mathrm{backwards}.\:\mathrm{The}\:\mathrm{respective}\:\mathrm{masses}\:\mathrm{of}\:\mathrm{the}\:\mathrm{fisherman}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{boat}\:\mathrm{are}\:\mathrm{85}.\mathrm{0}\:\mathrm{kg}\:\mathrm{and}\:\mathrm{165}\:\mathrm{kg}\:\mathrm{and}\:\mathrm{the}\:\mathrm{frictional}\:\mathrm{force}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{boat}\:\mathrm{and}\:\mathrm{water}\:\mathrm{is}\:\mathrm{negligible}.\:\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{fisherman}\:\mathrm{and}\:\mathrm{the}\:\mathrm{both}\:\mathrm{at}\:\mathrm{the}\:\mathrm{instant}\:\mathrm{when}\:\mathrm{he}\:\mathrm{just}\:\mathrm{lands}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{shore}? \\ $$
Answered by mr W last updated on 28/Apr/21

$$\left(\mathrm{1}+\frac{\mathrm{85}}{\mathrm{165}}\right)×\mathrm{0}.\mathrm{65}\approx\mathrm{0}.\mathrm{98}{m} \\ $$
Commented by physicstutes last updated on 28/Apr/21
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{have}\:\mathrm{you}\:\mathrm{accounted}\:\mathrm{for}\:\mathrm{the}\:\mathrm{speed} \\ $$
Commented by mr W last updated on 28/Apr/21

$${as}\:{far}\:{as}\:{no}\:{external}\:{force}\:{acts}\:{on} \\ $$$${an}\:{object}\:{in}\:{a}\:{certain}\:{direction},\:{the} \\ $$$${object}\:{won}'{t}\:{change}\:{its}\:{position}\:{in} \\ $$$${this}\:{direction}.\:{that}'{s}\:{clear}. \\ $$$${on}\:{the}\:{object}\:“{boat}+{fisherman}''\:{no} \\ $$$${external}\:{force}\:{acts}\:{in}\:{horizontal} \\ $$$${direction},\:{therefore}\:{it}\:{doesn}'{t}\:{change} \\ $$$${its}\:{horizontal}\:{position},\:{i}.{e}.\:{the}\: \\ $$$${center}\:{of}\:{mass}\:{from}\:“{boat}+\:{fisherman}'' \\ $$$${keeps}\:{unchanged}\:{when}\:{the}\:{man} \\ $$$${jumps}\:{from}\:{boat}\:{onto}\:{the}\:{shore}. \\ $$$${the}\:{center}\:{of}\:{mass}\:{of}\:“{boat}\:+\:{fisherman}'' \\ $$$${was}\:\mathrm{0}.\mathrm{65}{m}\:{apart}\:{from}\:{the}\:{shore}. \\ $$$${at}\:{the}\:{moment}\:{when}\:{the}\:{fisherman} \\ $$$${reaches}\:{the}\:{shore},\:{the}\:{fisherman} \\ $$$${is}\:\mathrm{0}.\mathrm{65}{m}\:{away}\:{from}\:{the}\:{center}\:{of} \\ $$$${mass},\:{the}\:{boat}\:{must}\:{be}\:\frac{\mathrm{85}}{\mathrm{165}}×\mathrm{0}.\mathrm{65}{m} \\ $$$${away}\:{from}\:{the}\:{center}\:{of}\:{mass},\:{but} \\ $$$${in}\:{opposite}\:{direction},\:{so}\:{the}\:{distance} \\ $$$${from}\:{fisherman}\:{to}\:{the}\:{boat}\:{is} \\ $$$$\mathrm{0}.\mathrm{65}+\frac{\mathrm{85}}{\mathrm{165}}×\mathrm{0}.\mathrm{65}\approx\mathrm{0}.\mathrm{98}{m}. \\ $$
Commented by physicstutes last updated on 28/Apr/21

$$\mathrm{sir}\:\mathrm{the}\:\mathrm{boat}\:\mathrm{is}\:\mathrm{said}\:\mathrm{to}\:\boldsymbol{{move}}\:\boldsymbol{{backward}}\:\mathrm{therefore}\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:\mathrm{force} \\ $$$$\mathrm{involved}\:\mathrm{right}? \\ $$$$\:\mathrm{equal}\:\mathrm{and}\:\mathrm{opposite}\:\mathrm{forces}.\:\mathrm{the}\:\mathrm{man}\:\mathrm{gets}\:\mathrm{a}\:\mathrm{force}\:\mathrm{to}\:\mathrm{move}\:\mathrm{to}\:\mathrm{the}\:\mathrm{shore}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{boat}\:\mathrm{gains}\:\mathrm{an}\:\mathrm{opposite}\:\mathrm{force}\:\mathrm{to}\:\mathrm{move}\:\mathrm{backwards}..\mathrm{but}\:\mathrm{accelerations}\:\mathrm{will} \\ $$$$\mathrm{not}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{since}\:\mathrm{masses}\:\mathrm{are}\:\mathrm{different}.\:\mathrm{right}? \\ $$
Commented by mr W last updated on 29/Apr/21
Commented by mr W last updated on 29/Apr/21

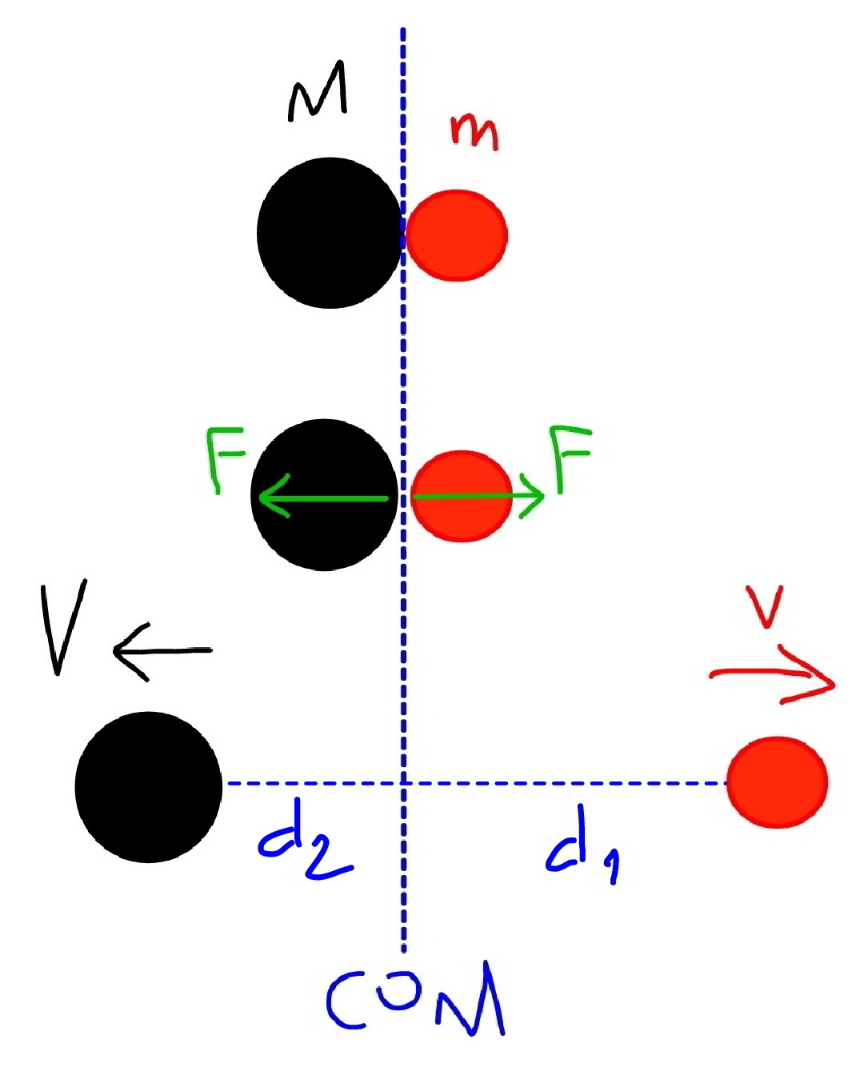
$${black}={boat} \\ $$$${red}={fisherman} \\ $$$${COM}={center}\:{of}\:{mass}\:{from}\:{boat}\:\&\:{man} \\ $$$${when}\:{the}\:{man}\:{jumps}\:{from}\:{the}\:{boat}, \\ $$$${he}\:{acts}\:{a}\:{force}\:{to}\:{the}\:{boat},\:{this}\:{force} \\ $$$${makes}\:{the}\:{boat}\:{to}\:{move}\:{to}\:{left},\:{but} \\ $$$${the}\:{boat}\:{acts}\:{also}\:{the}\:{same}\:{force}\:{in}\: \\ $$$${opposite}\:{direction}\:{to}\:{the}\:{man}\:{and} \\ $$$${makes}\:{ihm}\:{to}\:{move}\:{to}\:{right}.\:{both} \\ $$$${forces}\:{are}\:{internal}\:{forces}\:{inside} \\ $$$${the}\:{object}\:“{boat}\:\&\:{fisherman}''.\:{on} \\ $$$${the}\:{object}\:“{boat}\:\&\:{fisherman}''\:{itself} \\ $$$${no}\:{extermal}\:{force}\:{acts}\:{in}\:{this}\: \\ $$$${process},\:{therefore}\:{the}\:{COM}\:{of}\:{the} \\ $$$${object}\:“{boat}\:\&\:{fisherman}''\:{remains} \\ $$$${unchanged}. \\ $$
Commented by mr W last updated on 29/Apr/21

$${if}\:{one}\:{really}\:{understands}\:{the}\:{physics}, \\ $$$${he}\:{sees}\:{the}\:{boat}\:{and}\:{the}\:{fisherman} \\ $$$${as}\:{a}\:{single}\:{object}\:{and}\:{that}\:{this}\:{object} \\ $$$${doesn}'{t}\:{move},\:{although}\:{both}\:{boat}\:{and} \\ $$$${fisherman}\:{are}\:{in}\:{motion}.\:{with}\:{this} \\ $$$${understanding}\:{he}\:{gets}\:{the}\:{correct} \\ $$$${result}\:{without}\:{much}\:{calculation}. \\ $$$$ \\ $$$${if}\:{one}\:{is}\:{good}\:{in}\:{physics},\:{he}\:{knows} \\ $$$${how}\:{to}\:{calculate}\:{to}\:{get}\:{the}\:{correct} \\ $$$${result}.\:{here}\:{is}\:{how}\:{to}\:{calculate}: \\ $$$${say}\:{F}\:{is}\:{the}\:{force}\:{between}\:{boat}\:{and} \\ $$$${fisherman}\:{as}\:{he}\:{jumps}\:{from}\:{boat}. \\ $$$${say}\:{this}\:{force}\:{acts}\:{in}\:{a}\:{short}\:{time}\:\Delta{t}. \\ $$$${V}={speed}\:{of}\:{boat}\:\left({to}\:{left}\right) \\ $$$${v}={speed}\:{of}\:{fisherman}\:\left({to}\:{right}\right) \\ $$$${MV}={F}\Delta{t} \\ $$$${mv}={F}\Delta{t} \\ $$$${MV}={mv} \\ $$$$\Rightarrow\frac{{V}}{{v}}=\frac{{m}}{{M}} \\ $$$${the}\:{fisherman}\:{moves}\:{d}_{\mathrm{1}} =\mathrm{0}.\mathrm{65}{m}\:{in} \\ $$$${time}\:{t}=\frac{{d}_{\mathrm{1}} }{{v}}.\:{in}\:{this}\:{time}\:{the}\:{boat}\:{moves} \\ $$$${d}_{\mathrm{2}} ={Vt}={V}×\frac{{d}_{\mathrm{1}} }{{v}}=\frac{{V}}{{v}}×{d}_{\mathrm{1}} =\frac{{m}}{{V}}×{d}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{85}}{\mathrm{165}}×\mathrm{0}.\mathrm{65} \\ $$$${the}\:{distance}\:{between}\:{both}\:{is}\:{then} \\ $$$${d}_{\mathrm{1}} +{d}_{\mathrm{2}} =\mathrm{0}.\mathrm{65}+\frac{\mathrm{85}}{\mathrm{165}}×\mathrm{0}.\mathrm{65}\approx\mathrm{0}.\mathrm{98}{m}. \\ $$
Commented by peter frank last updated on 29/Apr/21
$${thank}\:{you} \\ $$
