Question Number 6246 by FilupSmith last updated on 20/Jun/16
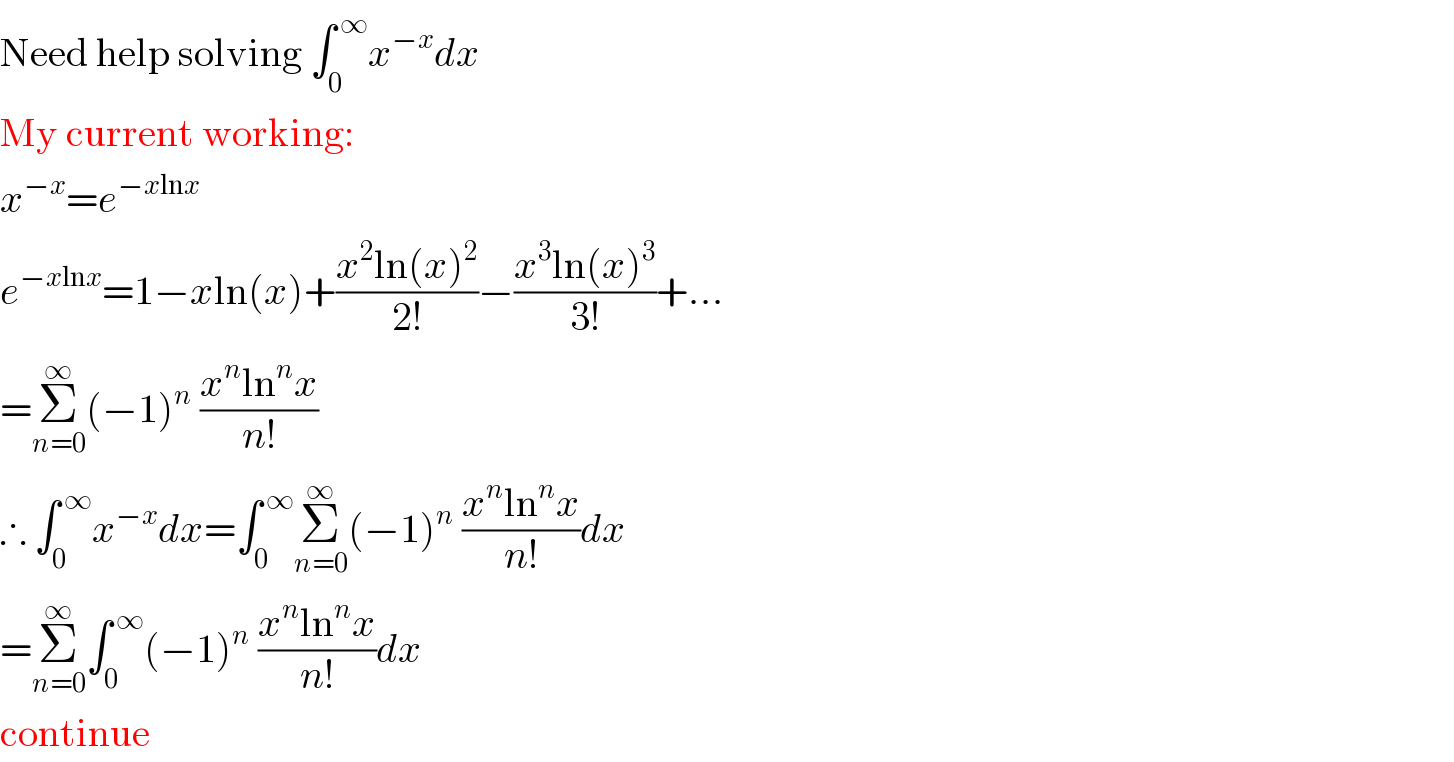
$$\mathrm{Need}\:\mathrm{help}\:\mathrm{solving}\:\int_{\mathrm{0}} ^{\:\infty} {x}^{−{x}} {dx} \\ $$$$\mathrm{My}\:\mathrm{current}\:\mathrm{working}: \\ $$$${x}^{−{x}} ={e}^{−{x}\mathrm{ln}{x}} \\ $$$${e}^{−{x}\mathrm{ln}{x}} =\mathrm{1}−{x}\mathrm{ln}\left({x}\right)+\frac{{x}^{\mathrm{2}} \mathrm{ln}\left({x}\right)^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} \mathrm{ln}\left({x}\right)^{\mathrm{3}} }{\mathrm{3}!}+… \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\frac{{x}^{{n}} \mathrm{ln}^{{n}} {x}}{{n}!} \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\:\infty} {x}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\:\infty} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\frac{{x}^{{n}} \mathrm{ln}^{{n}} {x}}{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\infty} \left(−\mathrm{1}\right)^{{n}} \:\frac{{x}^{{n}} \mathrm{ln}^{{n}} {x}}{{n}!}{dx} \\ $$$$\mathrm{continue} \\ $$
Commented by FilupSmith last updated on 20/Jun/16

$$\mathrm{after}\:\mathrm{solving}\:\mathrm{similarly}\:\mathrm{to}\:\int{x}^{{x}} {dx} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−{x}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left(−{n}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)^{−\left({n}+\mathrm{1}\right)} \int_{−\infty} ^{\:\infty} {e}^{−{u}} {u}^{{n}} {du} \\ $$
