Question Number 142318 by mnjuly1970 last updated on 29/May/21
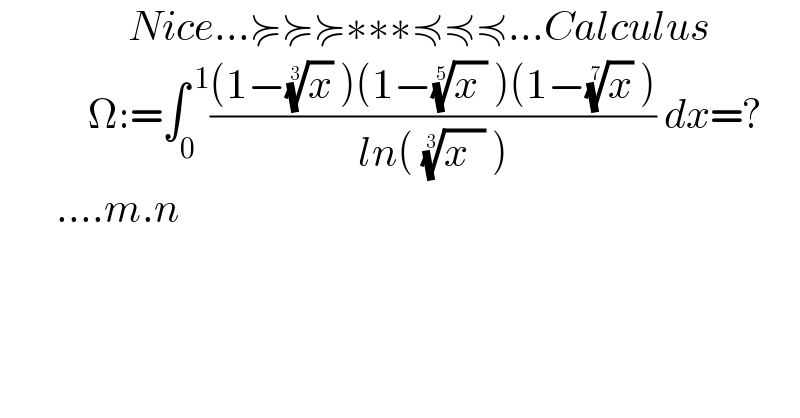
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Nice}…\succcurlyeq\succcurlyeq\succcurlyeq\ast\ast\ast\preccurlyeq\preccurlyeq\preccurlyeq…{Calculus} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Omega:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\sqrt[{\mathrm{3}}]{{x}}\:\right)\left(\mathrm{1}−\sqrt[{\mathrm{5}}]{{x}\:}\:\right)\left(\mathrm{1}−\sqrt[{\mathrm{7}}]{{x}}\:\right)}{{ln}\left(\:\sqrt[{\mathrm{3}}]{{x}\:\:}\:\right)}\:{dx}=? \\ $$$$\:\:\:\:\:\:\:….{m}.{n} \\ $$
Answered by Dwaipayan Shikari last updated on 29/May/21
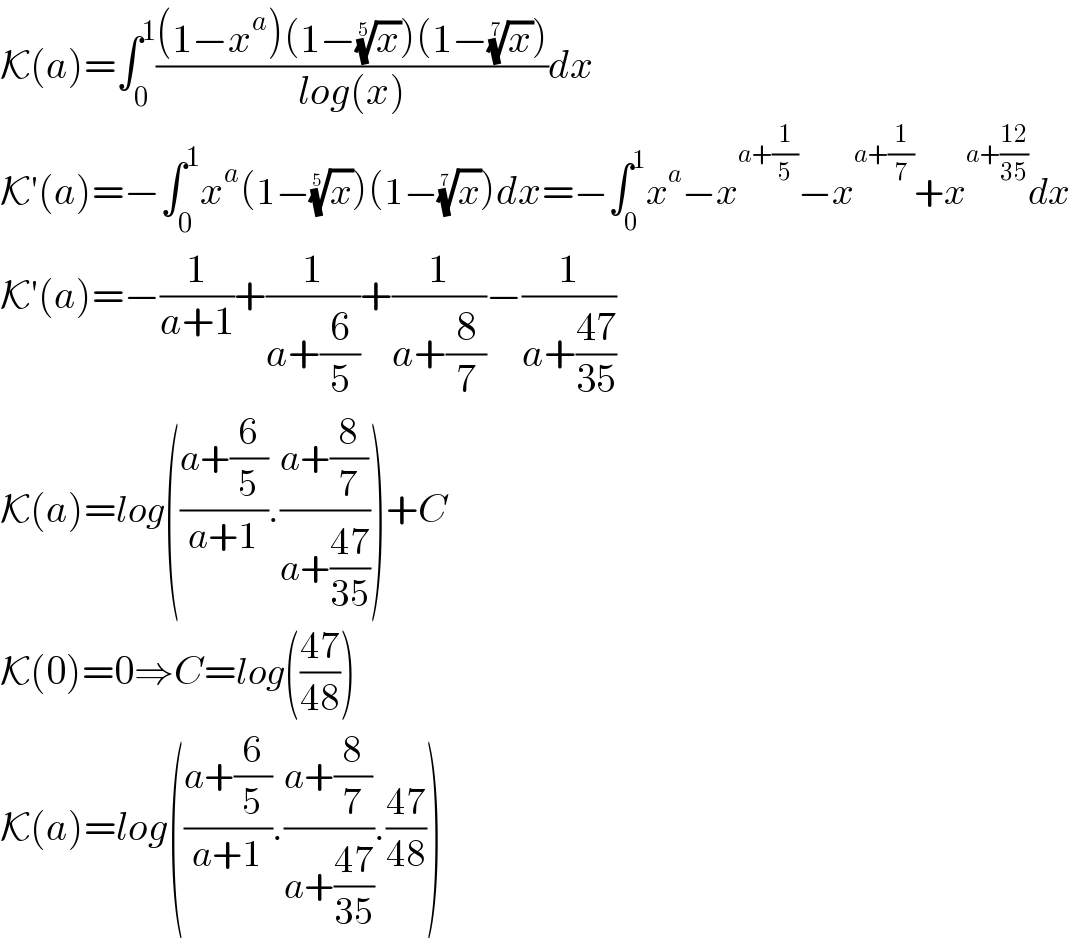
$$\mathcal{K}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}^{{a}} \right)\left(\mathrm{1}−\sqrt[{\mathrm{5}}]{{x}}\right)\left(\mathrm{1}−\sqrt[{\mathrm{7}}]{{x}}\right)}{{log}\left({x}\right)}{dx} \\ $$$$\mathcal{K}'\left({a}\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} \left(\mathrm{1}−\sqrt[{\mathrm{5}}]{{x}}\right)\left(\mathrm{1}−\sqrt[{\mathrm{7}}]{{x}}\right){dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} −{x}^{{a}+\frac{\mathrm{1}}{\mathrm{5}}} −{x}^{{a}+\frac{\mathrm{1}}{\mathrm{7}}} +{x}^{{a}+\frac{\mathrm{12}}{\mathrm{35}}} {dx} \\ $$$$\mathcal{K}'\left({a}\right)=−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{6}}{\mathrm{5}}}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{8}}{\mathrm{7}}}−\frac{\mathrm{1}}{{a}+\frac{\mathrm{47}}{\mathrm{35}}} \\ $$$$\mathcal{K}\left({a}\right)={log}\left(\frac{{a}+\frac{\mathrm{6}}{\mathrm{5}}}{{a}+\mathrm{1}}.\frac{{a}+\frac{\mathrm{8}}{\mathrm{7}}}{{a}+\frac{\mathrm{47}}{\mathrm{35}}}\right)+{C} \\ $$$$\mathcal{K}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{C}={log}\left(\frac{\mathrm{47}}{\mathrm{48}}\right) \\ $$$$\mathcal{K}\left({a}\right)={log}\left(\frac{{a}+\frac{\mathrm{6}}{\mathrm{5}}}{{a}+\mathrm{1}}.\frac{{a}+\frac{\mathrm{8}}{\mathrm{7}}}{{a}+\frac{\mathrm{47}}{\mathrm{35}}}.\frac{\mathrm{47}}{\mathrm{48}}\right) \\ $$
Commented by mnjuly1970 last updated on 29/May/21
$${thank}\:{you}\:{so}\:{much}… \\ $$
