Question Number 137474 by mnjuly1970 last updated on 03/Apr/21
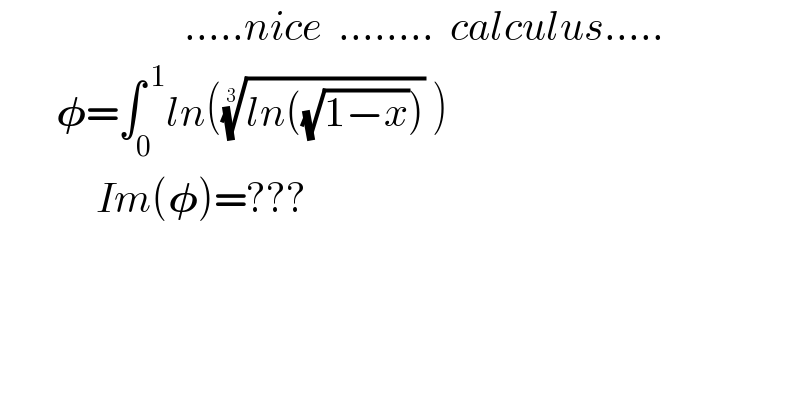
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..{nice}\:\:……..\:\:{calculus}….. \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\sqrt[{\mathrm{3}}]{{ln}\left(\sqrt{\mathrm{1}−{x}}\right)}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{Im}\left(\boldsymbol{\phi}\right)=??? \\ $$
Answered by mindispower last updated on 03/Apr/21
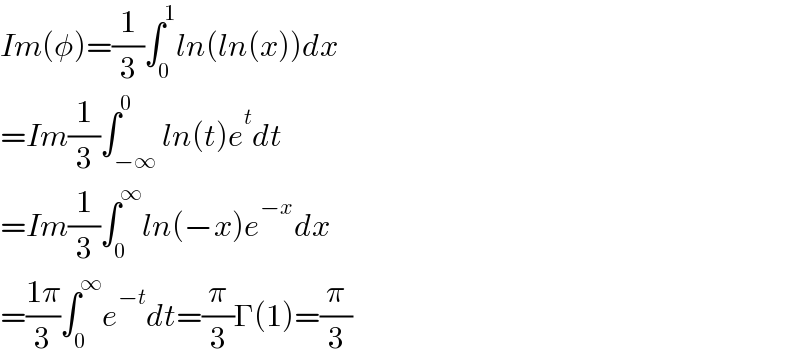
$${Im}\left(\phi\right)=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({ln}\left({x}\right)\right){dx} \\ $$$$={Im}\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{\mathrm{0}} {ln}\left({t}\right){e}^{{t}} {dt} \\ $$$$={Im}\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {ln}\left(−{x}\right){e}^{−{x}} {dx} \\ $$$$=\frac{\mathrm{1}\pi}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {dt}=\frac{\pi}{\mathrm{3}}\Gamma\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 03/Apr/21
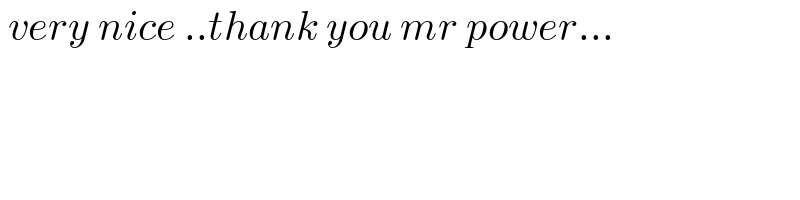
$$\:{very}\:{nice}\:..{thank}\:{you}\:{mr}\:{power}… \\ $$
Answered by Ñï= last updated on 03/Apr/21
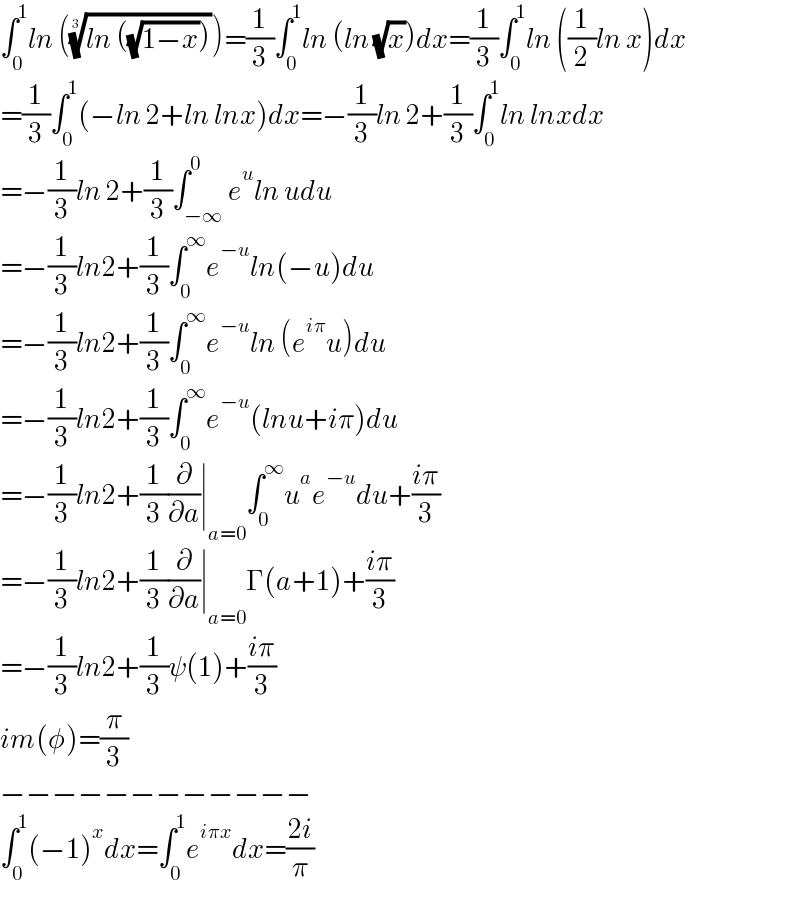
$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\:\left(\sqrt[{\mathrm{3}}]{{ln}\:\left(\sqrt{\mathrm{1}−{x}}\right)}\right)=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\:\left({ln}\:\sqrt{{x}}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\:{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−{ln}\:\mathrm{2}+{ln}\:{lnx}\right){dx}=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\:\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\:{lnxdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\:\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{\mathrm{0}} {e}^{{u}} {ln}\:{udu} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {ln}\left(−{u}\right){du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {ln}\:\left({e}^{{i}\pi} {u}\right){du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} \left({lnu}+{i}\pi\right){du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{0}} \int_{\mathrm{0}} ^{\infty} {u}^{{a}} {e}^{−{u}} {du}+\frac{{i}\pi}{\mathrm{3}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{0}} \Gamma\left({a}+\mathrm{1}\right)+\frac{{i}\pi}{\mathrm{3}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}}\psi\left(\mathrm{1}\right)+\frac{{i}\pi}{\mathrm{3}} \\ $$$${im}\left(\phi\right)=\frac{\pi}{\mathrm{3}} \\ $$$$−−−−−−−−−−−− \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{x}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{i}\pi{x}} {dx}=\frac{\mathrm{2}{i}}{\pi} \\ $$
Commented by mnjuly1970 last updated on 03/Apr/21

$${thanks}\:{alot}\:.. \\ $$
Answered by Dwaipayan Shikari last updated on 03/Apr/21
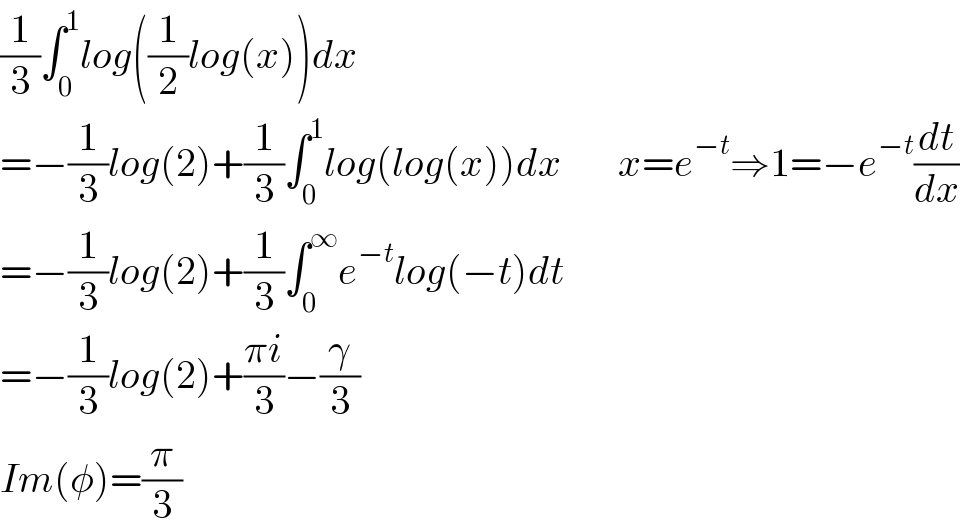
$$\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}\right)\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({log}\left({x}\right)\right){dx}\:\:\:\:\:\:\:{x}={e}^{−{t}} \Rightarrow\mathrm{1}=−{e}^{−{t}} \frac{{dt}}{{dx}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {log}\left(−{t}\right){dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)+\frac{\pi{i}}{\mathrm{3}}−\frac{\gamma}{\mathrm{3}} \\ $$$${Im}\left(\phi\right)=\frac{\pi}{\mathrm{3}} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Apr/21
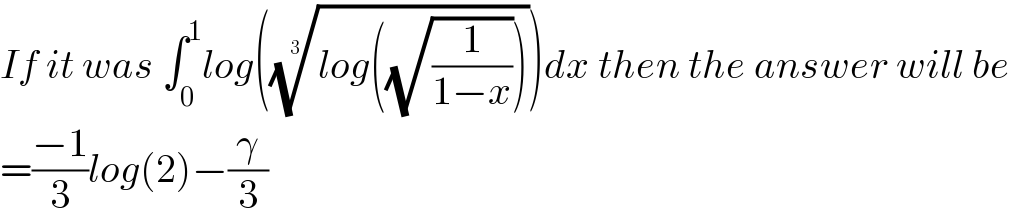
$${If}\:{it}\:{was}\:\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\sqrt[{\mathrm{3}}]{{log}\left(\sqrt{\frac{\mathrm{1}}{\mathrm{1}−{x}}}\right)}\right){dx}\:{then}\:{the}\:{answer}\:{will}\:{be} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)−\frac{\gamma}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 03/Apr/21
$$\:{grateful}\:{mr}\:{payan}… \\ $$
