Question Number 131875 by mnjuly1970 last updated on 09/Feb/21
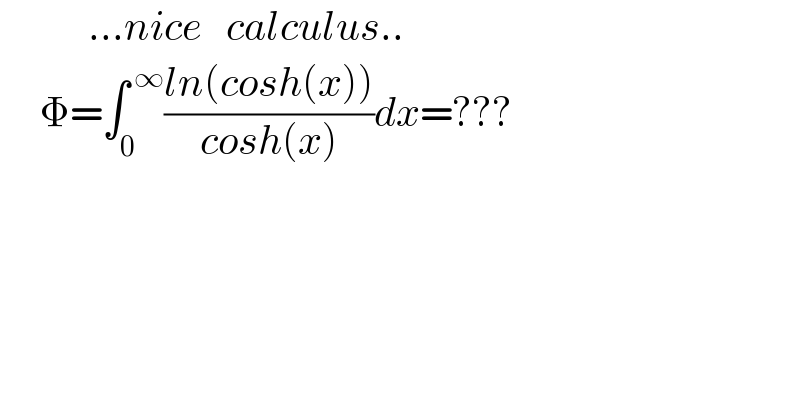
$$\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:\:{calculus}.. \\ $$$$\:\:\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({cosh}\left({x}\right)\right)}{{cosh}\left({x}\right)}{dx}=??? \\ $$
Answered by mindispower last updated on 09/Feb/21
![=∫_1 ^∞ ((ln(t)dt)/(t(√(t^2 −1)))) =∫_1 ^∞ ((ln(t).tdt)/(t^2 (√(t^2 −1))))=(1/4)∫_1 ^∞ ((ln(t)dt)/(t(√(t−1)))) t=(1/y)⇒(1/4)∫_0 ^1 ((−ln(y)dy)/( (√y).(√(1−y)))) =−(1/4)∫_0 ^1 ln(y)y^((1/2)−1) (1−y)^((1/2)−1) dy β(a,b)=∫_0 ^1 t^(a−1) (1−t)^(b−1) dt we find=−(1/4)∂_a β((1/2),(1/2))=−(1/4)β((1/2),(1/2))[Ψ((1/2))−Ψ(1)] =−(π/4)[−2ln(2)]=((πln(2))/2)](https://www.tinkutara.com/question/Q131927.png)
$$=\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({t}\right){dt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({t}\right).{tdt}}{{t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({t}\right){dt}}{{t}\sqrt{{t}−\mathrm{1}}} \\ $$$${t}=\frac{\mathrm{1}}{{y}}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{ln}\left({y}\right){dy}}{\:\sqrt{{y}}.\sqrt{\mathrm{1}−{y}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({y}\right){y}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dy} \\ $$$$\beta\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {dt} \\ $$$${we}\:{find}=−\frac{\mathrm{1}}{\mathrm{4}}\partial_{{a}} \beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\mathrm{1}}{\mathrm{4}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right] \\ $$$$=−\frac{\pi}{\mathrm{4}}\left[−\mathrm{2}{ln}\left(\mathrm{2}\right)\right]=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
