Menu Close

nice-calculus-compute-2li-2-1-2-2li-2-1-2-li-2-3-4-

Tinku Tara 0 Comments
Pin




Question Number 136170 by mnjuly1970 last updated on 19/Mar/21
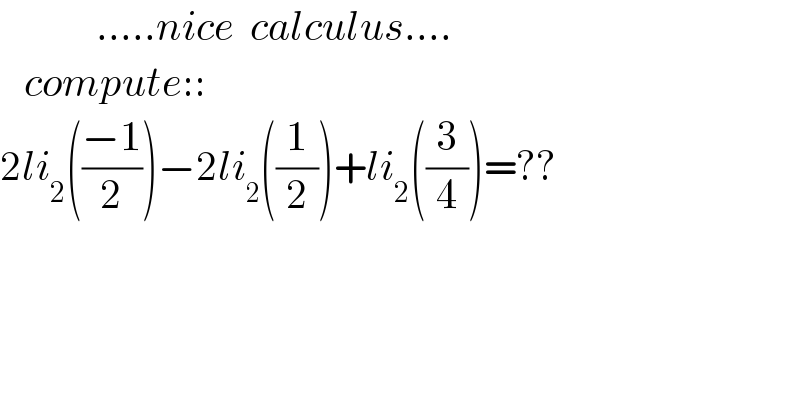
.....nice calculus.... compute:: 2li_2 (((−1)/2))−2li_2 ((1/2))+li_2 ((3/4))=??
$$\:\:\:\:\:\:\:\:\:\:\:\:…..{nice}\:\:{calculus}…. \\ $$$$\:\:\:{compute}:: \\ $$$$\mathrm{2}{li}_{\mathrm{2}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{li}_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)=?? \\ $$$$ \\ $$
Answered by mindispower last updated on 19/Mar/21
li_2 (−x)−li_2 (1−x)+((li_2 (1−x^2 ))/2)=−(π^2 /(12))−ln(x)ln(1+x)....T x=(1/2) ⇔2li_2 (−(1/2))−2li_2 ((1/2))+li_2 ((3/4))=−(π^2 /6)−ln((1/2))ln((3/2)) (T) True li_2 (x)=∫_0 ^x −((ln(1−t))/t)dt f(x)=2li_2 (−x)−2li_2 (1−x)+li_2 (1−x^2 ) f′(x)=2((ln(1+x))/(−x))−2((ln(x))/(1−x))+((2xln(x^2 ))/(1−x^2 )) ==−((2ln(1+x))/x)−((2ln(x))/(1−x))+((2ln(x))/(1−x))−((2ln(x))/(1+x)) =−2((ln(1+x))/x)−2((ln(x))/(1+x)) ∫((ln(x))/(1+x))=ln(x)ln(1+x)−∫((ln(1+x))/x)dx f(x)=−2((ln(1+x))/x)−2ln(x)ln(1+x)+2∫((ln(1+x))/x)dx =−2ln(x)ln(1+x)+c f(0)=c=2li_2 (0)−2li_2 (1)+li_2 (1) =−(π^2 /6) ⇒f(x)=2li_2 (−x)−2li_2 (1−x)+li_2 (1−x^2 )=−(π^2 /6)−2ln(x)ln(1+x) ⇔(T) true
$${li}_{\mathrm{2}} \left(−{x}\right)−{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\frac{{li}_{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{2}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)….{T} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{2}{li}_{\mathrm{2}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{li}_{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\left({T}\right)\:{True} \\ $$$${li}_{\mathrm{2}} \left({x}\right)=\int_{\mathrm{0}} ^{{x}} −\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$${f}\left({x}\right)=\mathrm{2}{li}_{\mathrm{2}} \left(−{x}\right)−\mathrm{2}{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$${f}'\left({x}\right)=\mathrm{2}\frac{{ln}\left(\mathrm{1}+{x}\right)}{−{x}}−\mathrm{2}\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}}+\frac{\mathrm{2}{xln}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$==−\frac{\mathrm{2}{ln}\left(\mathrm{1}+{x}\right)}{{x}}−\frac{\mathrm{2}{ln}\left({x}\right)}{\mathrm{1}−{x}}+\frac{\mathrm{2}{ln}\left({x}\right)}{\mathrm{1}−{x}}−\frac{\mathrm{2}{ln}\left({x}\right)}{\mathrm{1}+{x}} \\ $$$$=−\mathrm{2}\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}−\mathrm{2}\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}} \\ $$$$\int\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}={ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)−\int\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$${f}\left({x}\right)=−\mathrm{2}\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}−\mathrm{2}{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)+\mathrm{2}\int\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$$=−\mathrm{2}{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right)+{c} \\ $$$${f}\left(\mathrm{0}\right)={c}=\mathrm{2}{li}_{\mathrm{2}} \left(\mathrm{0}\right)−\mathrm{2}{li}_{\mathrm{2}} \left(\mathrm{1}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{li}_{\mathrm{2}} \left(−{x}\right)−\mathrm{2}{li}_{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{{x}}\right)+\boldsymbol{{li}}_{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{2}{ln}\left({x}\right){ln}\left(\mathrm{1}+{x}\right) \\ $$$$\Leftrightarrow\left({T}\right)\:{true} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 19/Mar/21
thanks alot...
$${thanks}\:{alot}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *