nice-calculus-evaluate-0-1-x-e-pi-1-x-e-1-ln-x-1-3-dx-3-pi-

Question Number 138742 by mnjuly1970 last updated on 17/Apr/21

\dots \dots . . n i c e \dots . c a l c u l u s \dots

e v a l u a t e ::

Ω = \int_{0}^{1} \frac{x^{e^{π} - 1} - x^{e^{γ} - 1}}{l n (\sqrt[3]{x})} d x \overset{?}{=} 3 (π - γ)

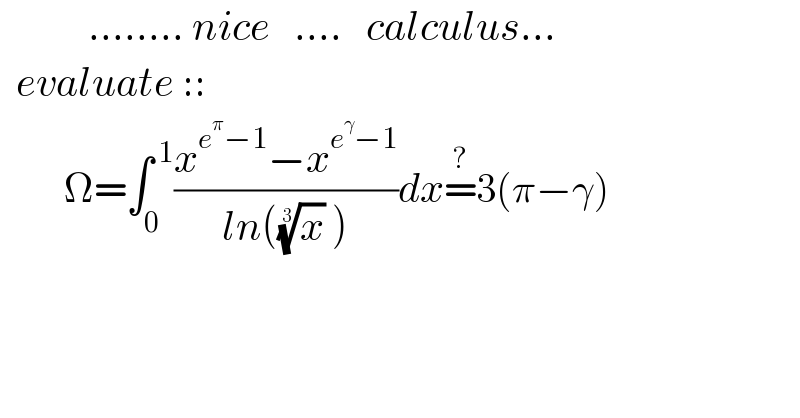
Answered by Dwaipayan Shikari last updated on 17/Apr/21

3 \int_{0}^{1} \frac{x^{e^{π} - 1} - x^{e^{γ} - 1}}{l o g (x)} d x = 3 χ (e^{π} - 1, e^{γ} - 1) = 3 (π - γ)

χ (a, b) = \int_{0}^{1} \frac{x^{a} - x^{b}}{l o g (x)} d x

\frac{\partial}{\partial a} χ (a, b) = \frac{1}{a + 1} \Rightarrow χ (a, b) = l o g (a + 1) + C

χ (b, b) = 0 \Rightarrow C = - l o g (b + 1) \Rightarrow χ (a, b) = l o g (\frac{a + 1}{b + 1})

Commented by Ar Brandon last updated on 17/Apr/21

Wow cool! I was supposed to remain at

the first power .

Commented by mnjuly1970 last updated on 17/Apr/21

t a s h a k o r \dots m e r c e y . .

Answered by Ar Brandon last updated on 17/Apr/21

Ω = \int_{0}^{1} \frac{x^{e^{π} - 1} - x^{e^{γ} - 1}}{\ln (\sqrt[3]{x})} dx, u = x^{\frac{1}{3}} \Rightarrow {3 u}^{2} du = dx

= \int_{0}^{1} \frac{u^{3 (e^{π} - 1)} - u^{3 (e^{γ} - 1)}}{\ln (u)} ({3 u}^{2} du) = 3 \int_{0}^{1} \frac{u^{{3 e}^{π} - 1} - u^{{3 e}^{γ} - 1}}{\ln (u)} du

f (α) = 3 \int_{0}^{1} \frac{u^{{3 e}^{π} + α} - u^{{3 e}^{γ} + α}}{\ln (u)} du

f^{'} (α) = 3 \int_{0}^{1} (u^{{3 e}^{π} + α} - u^{{3 e}^{γ} + α}) du

= 3 {[\frac{u^{{3 e}^{π} + α + 1}}{{3 e}^{π} + α + 1} - \frac{u^{{3 e}^{γ} + α + 1}}{{3 e}^{γ} + α + 1}]}_{0}^{1}

= 3 [\frac{1}{{3 e}^{π} + α + 1} - \frac{1}{{3 e}^{γ} + α + 1}]

f (α) = 3 \ln ({3 e}^{π} + α + 1) - 3 \ln ({3 e}^{γ} + α + 1) + C

Commented by mnjuly1970 last updated on 17/Apr/21

t h a n k s a l o t \dots