Menu Close

nice-calculus-evaluation-of-0-xe-x-1-e-x-dx-solution-1-e-x-t-x-ln-1-t-e-x-dx-dt-0-

Tinku Tara 0 Comments
Pin




Question Number 135525 by mnjuly1970 last updated on 13/Mar/21
.... nice ................ calculus... evaluation of :: 𝛗=∫_0 ^( ∞) xe^(βˆ’x) (√(1βˆ’e^(βˆ’x) )) dx solution:: 1βˆ’e^(βˆ’x) =t β‡’ {_( x=βˆ’ln(1βˆ’t)) ^( e^(βˆ’x) dx=dt) 𝛗=βˆ’βˆ«_0 ^( 1) ln(1βˆ’t).t^(1/2) dt =∫_0 ^( 1) Ξ£_(n=1) ^∞ (t^(n+(1/2)) /n)dt=Ξ£_(n=1) ^∞ (1/(n(n+(3/2)))) .... ∴ 𝛗= Ξ£_(n=1) ^∞ (1/(n(n+(3/2))))=Ξ£_(n=1) ^∞ (1/n)βˆ’(1/(n+(3/2))) .... =(2/3){Ξ³βˆ’Ξ³+Ξ£_(n=1) ^∞ ((1/n)βˆ’(1/(n+(3/2))))} .... we know that : ψ(s+1) := βˆ’Ξ³+Ξ£_(n=1) ^∞ ((1/n)βˆ’(1/(n+s))) ..... ∴ 𝛗=(2/3)(Ξ³+ψ((5/2))) .... on the oyher hand we have:: ψ(s+1)=(1/s)+ψ(s) ...... ψ((1/2))=βˆ’Ξ³βˆ’2ln(2) ...... ψ((5/2))=(2/3)+ψ((3/2))=(2/3)+(2+ψ((1/2))) =(2/3)+2+(βˆ’Ξ³βˆ’2ln(2)) .... ∴ ψ((3/2))=(8/3)βˆ’Ξ³βˆ’ln(4) .... :::::: 𝛗 =(2/3)(Ξ³+(8/3)βˆ’Ξ³βˆ’ln(4)) .... 𝛗=(2/3)((8/3)βˆ’ln(4))=(4/3)((4/3)βˆ’ln(2)) .... ...... 𝛗= (4/3)((4/3)βˆ’ln(2))......βœ“βœ“ .... ... prepare by mr rizzyβˆ’aka... solution with detais :m.n.july.1970
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:{nice}\:…………….\:{calculus}… \\ $$$$\:\:\:\:\:{evaluation}\:{of}\:::\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} {xe}^{βˆ’{x}} \sqrt{\mathrm{1}βˆ’{e}^{βˆ’{x}} }\:{dx} \\ $$$$\:\:\:\:{solution}::\: \\ $$$$\:\:\:\:\mathrm{1}βˆ’{e}^{βˆ’{x}} ={t}\:\:\Rightarrow\:\left\{_{\:{x}=βˆ’{ln}\left(\mathrm{1}βˆ’{t}\right)} ^{\:{e}^{βˆ’{x}} {dx}={dt}} \right. \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}=βˆ’\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\mathrm{1}βˆ’{t}\right).{t}^{\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{{n}}{dt}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:…. \\ $$$$\:\:\:\:\:\:\:\:\therefore\:\:\boldsymbol{\phi}=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}βˆ’\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}}{\mathrm{2}}}\:…. \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}\left\{\gammaβˆ’\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}βˆ’\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}}{\mathrm{2}}}\right)\right\}\:…. \\ $$$$\:\:\:\:\:{we}\:{know}\:{that}\::\: \\ $$$$\:\:\:\:\:\:\:\psi\left({s}+\mathrm{1}\right)\::=\:βˆ’\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}βˆ’\frac{\mathrm{1}}{{n}+{s}}\right)\:….. \\ $$$$\:\:\:\:\:\:\:\:\:\therefore\:\boldsymbol{\phi}=\frac{\mathrm{2}}{\mathrm{3}}\left(\gamma+\psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\right)\:…. \\ $$$$\:\:\:\:\:\:\:\:\:{on}\:{the}\:{oyher}\:{hand}\:{we}\:{have}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\psi\left({s}+\mathrm{1}\right)=\frac{\mathrm{1}}{{s}}+\psi\left({s}\right)\:…… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=βˆ’\gammaβˆ’\mathrm{2}{ln}\left(\mathrm{2}\right)\:…… \\ $$$$\:\:\:\:\:\:\:\:\:\psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{3}}+\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{3}}+\left(\mathrm{2}+\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}+\left(βˆ’\gammaβˆ’\mathrm{2}{ln}\left(\mathrm{2}\right)\right)\:…. \\ $$$$\:\:\:\:\:\:\:\:\therefore\:\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{8}}{\mathrm{3}}βˆ’\gammaβˆ’{ln}\left(\mathrm{4}\right)\:…. \\ $$$$\:\:\:\:\:\:\:\:\:::::::\:\:\:\:\:\boldsymbol{\phi}\:=\frac{\mathrm{2}}{\mathrm{3}}\left(\gamma+\frac{\mathrm{8}}{\mathrm{3}}βˆ’\gammaβˆ’{ln}\left(\mathrm{4}\right)\right)\:…. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{8}}{\mathrm{3}}βˆ’{ln}\left(\mathrm{4}\right)\right)=\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{4}}{\mathrm{3}}βˆ’{ln}\left(\mathrm{2}\right)\right)\:…. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……\:\boldsymbol{\phi}=\:\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{4}}{\mathrm{3}}βˆ’{ln}\left(\mathrm{2}\right)\right)……\checkmark\checkmark\:…. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{prepare}\:{by}\:{mr}\:{rizzy}βˆ’{aka}… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{solution}\:{with}\:{detais}\::{m}.{n}.{july}.\mathrm{1970} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\: \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 13/Mar/21
Ξ΄(a)=∫_0 ^1 t^(1/2) (1βˆ’t)^(aβˆ’1) dtβ‡’((βˆ‚Ξ΄(a))/βˆ‚a)=∫_0 ^1 t^(1/2) (1βˆ’t)^(aβˆ’1) log(1βˆ’t)dt ((βˆ‚Ξ΄(a))/βˆ‚a)=(βˆ‚/βˆ‚a)(((Ξ“((3/2))Ξ“(a))/(Ξ“(a+(3/2)))))=((βˆšΟ€)/2)(((Ξ“(a+(3/2))Ξ“β€²(a)βˆ’Ξ“β€²(a+(3/2))Ξ“(a))/(Ξ“^2 (a+(3/2))))) a=1 =((βˆšΟ€)/2)(((βˆ’((3(βˆšΟ€))/4)Ξ³βˆ’((3(βˆšΟ€))/4)(βˆ’Ξ³+(8/3)βˆ’2log(2)))/((9Ο€)/(16)))) =(2/3)(log(4)βˆ’(8/3)) βˆ’Ξ΄β€²(1)=(2/3)((8/3)βˆ’log(4))
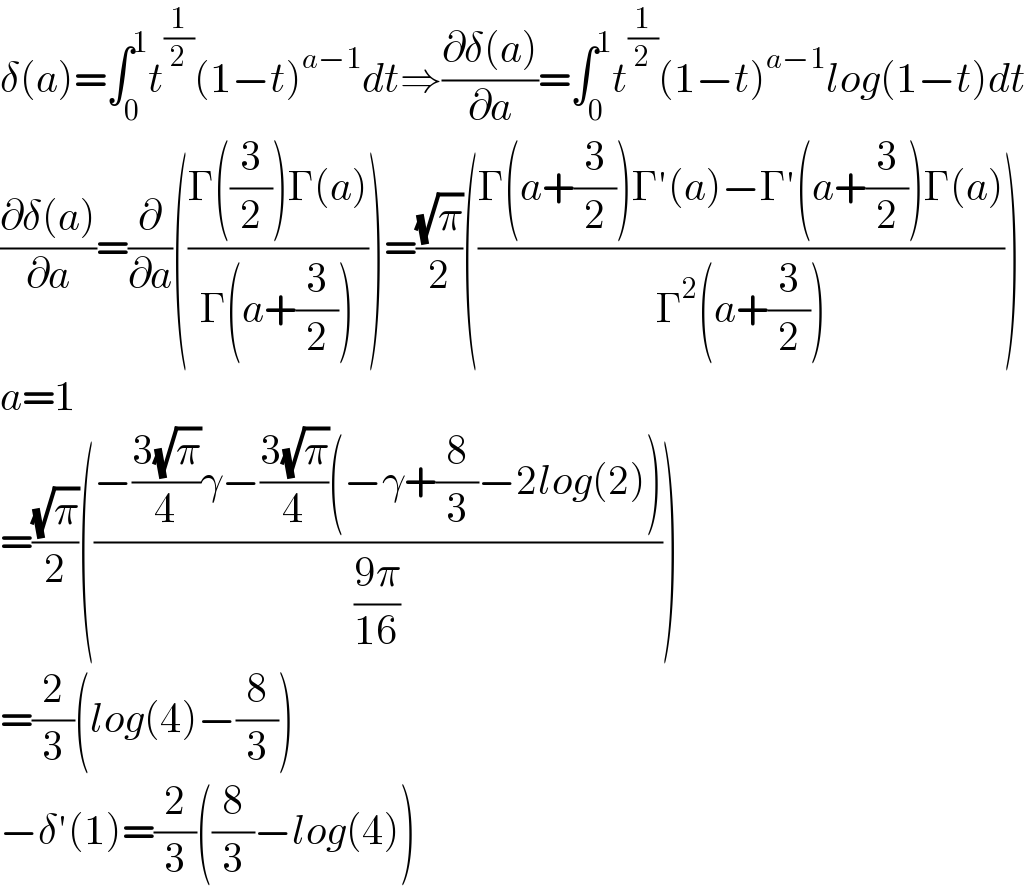
$$\delta\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}βˆ’{t}\right)^{{a}βˆ’\mathrm{1}} {dt}\Rightarrow\frac{\partial\delta\left({a}\right)}{\partial{a}}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}βˆ’{t}\right)^{{a}βˆ’\mathrm{1}} {log}\left(\mathrm{1}βˆ’{t}\right){dt} \\ $$$$\frac{\partial\delta\left({a}\right)}{\partial{a}}=\frac{\partial}{\partial{a}}\left(\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left({a}\right)}{\Gamma\left({a}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\Gamma\left({a}+\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma'\left({a}\right)βˆ’\Gamma'\left({a}+\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left({a}\right)}{\Gamma^{\mathrm{2}} \left({a}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right) \\ $$$${a}=\mathrm{1} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{βˆ’\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}\gammaβˆ’\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}\left(βˆ’\gamma+\frac{\mathrm{8}}{\mathrm{3}}βˆ’\mathrm{2}{log}\left(\mathrm{2}\right)\right)}{\frac{\mathrm{9}\pi}{\mathrm{16}}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left({log}\left(\mathrm{4}\right)βˆ’\frac{\mathrm{8}}{\mathrm{3}}\right) \\ $$$$βˆ’\delta'\left(\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{8}}{\mathrm{3}}βˆ’{log}\left(\mathrm{4}\right)\right) \\ $$
Commented by mnjuly1970 last updated on 13/Mar/21
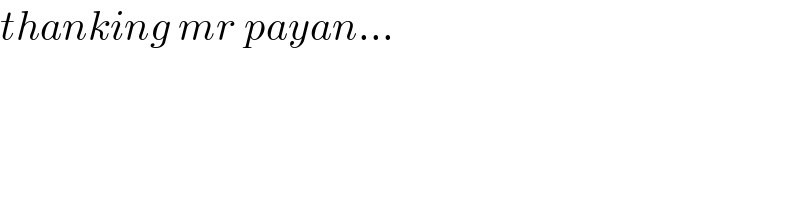
thanking mr payan...
$${thanking}\:{mr}\:{payan}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *