Question Number 133107 by mnjuly1970 last updated on 18/Feb/21
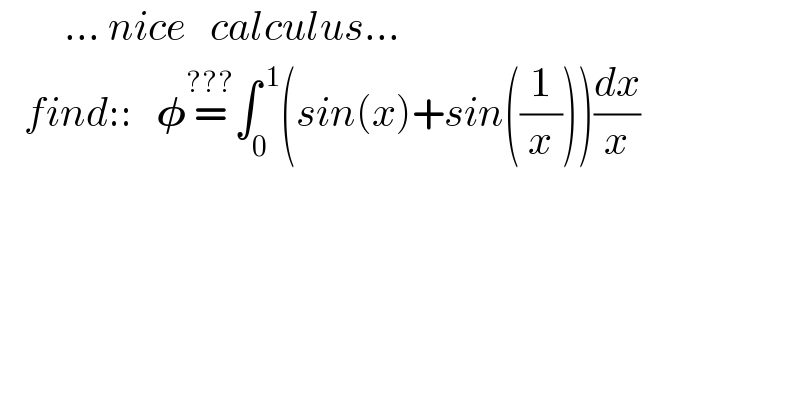
$$\:\:\:\:\:\:\:\:…\:{nice}\:\:\:{calculus}… \\ $$$$\:\:\:{find}::\:\:\:\boldsymbol{\phi}\overset{???} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({sin}\left({x}\right)+{sin}\left(\frac{\mathrm{1}}{{x}}\right)\right)\frac{{dx}}{{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Feb/21
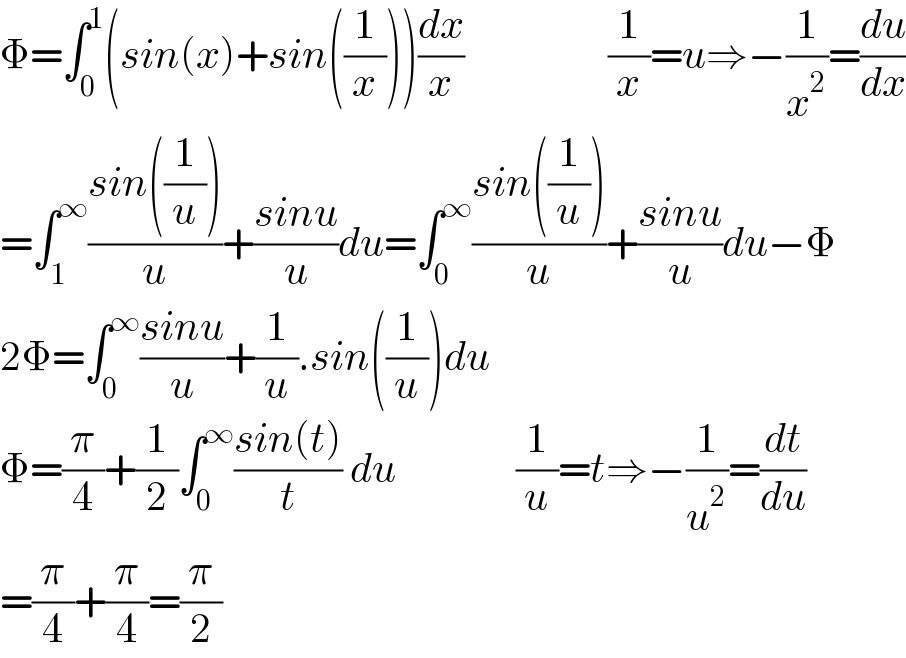
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \left({sin}\left({x}\right)+{sin}\left(\frac{\mathrm{1}}{{x}}\right)\right)\frac{{dx}}{{x}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}}={u}\Rightarrow−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\frac{{du}}{{dx}} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{sin}\left(\frac{\mathrm{1}}{{u}}\right)}{{u}}+\frac{{sinu}}{{u}}{du}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\frac{\mathrm{1}}{{u}}\right)}{{u}}+\frac{{sinu}}{{u}}{du}−\Phi \\ $$$$\mathrm{2}\Phi=\int_{\mathrm{0}} ^{\infty} \frac{{sinu}}{{u}}+\frac{\mathrm{1}}{{u}}.{sin}\left(\frac{\mathrm{1}}{{u}}\right){du} \\ $$$$\Phi=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}\:{du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{u}}={t}\Rightarrow−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }=\frac{{dt}}{{du}} \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 19/Feb/21
$${grateful}\:{mr}\:{payan}… \\ $$
