Question Number 141560 by mnjuly1970 last updated on 20/May/21
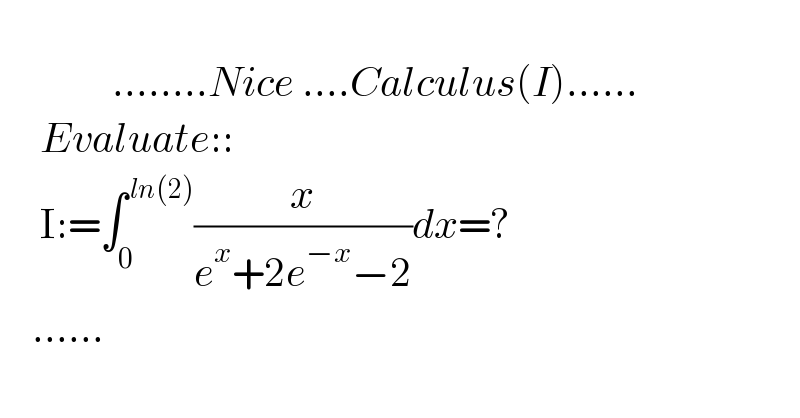
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..{Nice}\:….{Calculus}\left({I}\right)…… \\ $$$$\:\:\:\:\:{Evaluate}::\:\: \\ $$$$\:\:\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:{ln}\left(\mathrm{2}\right)} \frac{{x}}{{e}^{{x}} +\mathrm{2}{e}^{−{x}} −\mathrm{2}}{dx}=? \\ $$$$\:\:\:\:…… \\ $$
Answered by mindispower last updated on 20/May/21
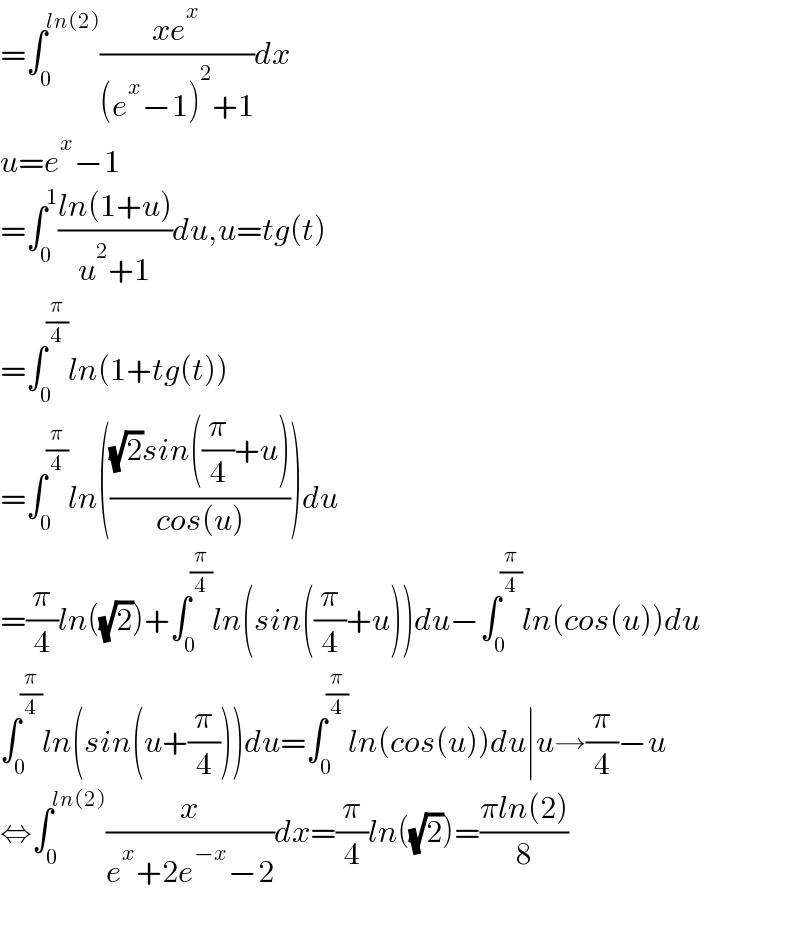
$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \frac{{xe}^{{x}} }{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${u}={e}^{{x}} −\mathrm{1} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} +\mathrm{1}}{du},{u}={tg}\left({t}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left({t}\right)\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\sqrt{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{4}}+{u}\right)}{{cos}\left({u}\right)}\right){du} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left(\sqrt{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left(\frac{\pi}{\mathrm{4}}+{u}\right)\right){du}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({u}\right)\right){du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left({u}+\frac{\pi}{\mathrm{4}}\right)\right){du}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({u}\right)\right){du}\mid{u}\rightarrow\frac{\pi}{\mathrm{4}}−{u} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \frac{{x}}{{e}^{{x}} +\mathrm{2}{e}^{−{x}} −\mathrm{2}}{dx}=\frac{\pi}{\mathrm{4}}{ln}\left(\sqrt{\mathrm{2}}\right)=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 20/May/21
$$\:\:\:\:{grateful}\:{sir}\:{power}… \\ $$
Commented by mindispower last updated on 20/May/21

$${pleasur}\:{sir} \\ $$
