Question Number 133443 by mnjuly1970 last updated on 22/Feb/21
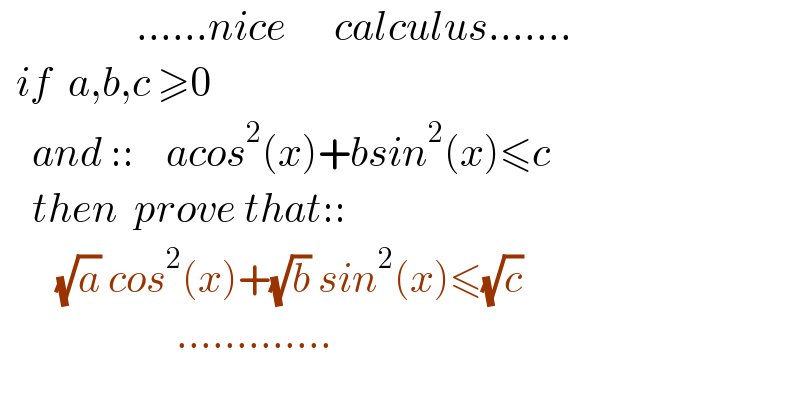
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……{nice}\:\:\:\:\:\:{calculus}……. \\ $$$$\:\:{if}\:\:{a},{b},{c}\:\geqslant\mathrm{0} \\ $$$$\:\:\:\:{and}\:::\:\:\:\:{acos}^{\mathrm{2}} \left({x}\right)+{bsin}^{\mathrm{2}} \left({x}\right)\leqslant{c} \\ $$$$\:\:\:\:{then}\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\:\:\sqrt{{a}}\:{cos}^{\mathrm{2}} \left({x}\right)+\sqrt{{b}}\:{sin}^{\mathrm{2}} \left({x}\right)\leqslant\sqrt{{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…………. \\ $$
Answered by mnjuly1970 last updated on 22/Feb/21
![u_1 ^→ =((√a) cos(x),(√b) sin(x))∈R^2 u_2 ^→ =(cos(x),sin(x))∈R^2 ∣u_1 ^→ .u_2 ^→ ∣≤_(schwartz) ^(cauchy) ∣u_1 ^→ ∣∣u_2 ^→ ∣ ∣(√a) cos^2 (x)+(√b) sin^2 (x)∣≤(√(acos^2 (x)+bsin^2 (x))) .(√([cos^2 (x)+sin^2 (x)]=1)) ∣(√a) cos^2 (x)+(√b) sin^2 (x)∣≤(√c) .....](https://www.tinkutara.com/question/Q133481.png)
$$\:\:\overset{\rightarrow} {{u}}_{\mathrm{1}} =\left(\sqrt{{a}}\:{cos}\left({x}\right),\sqrt{{b}}\:{sin}\left({x}\right)\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$$\:\:\:\overset{\rightarrow} {{u}}_{\mathrm{2}} =\left({cos}\left({x}\right),{sin}\left({x}\right)\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$$\:\:\:\:\mid\overset{\rightarrow} {{u}}_{\mathrm{1}} .\overset{\rightarrow} {{u}}_{\mathrm{2}} \mid\underset{{schwartz}} {\overset{{cauchy}} {\leqslant}}\mid\overset{\rightarrow} {{u}}_{\mathrm{1}} \mid\mid\overset{\rightarrow} {{u}}_{\mathrm{2}} \mid \\ $$$$\:\:\:\:\mid\sqrt{{a}}\:{cos}^{\mathrm{2}} \left({x}\right)+\sqrt{{b}}\:{sin}^{\mathrm{2}} \left({x}\right)\mid\leqslant\sqrt{{acos}^{\mathrm{2}} \left({x}\right)+{bsin}^{\mathrm{2}} \left({x}\right)}\:.\sqrt{\left[{cos}^{\mathrm{2}} \left({x}\right)+{sin}^{\mathrm{2}} \left({x}\right)\right]=\mathrm{1}} \\ $$$$\:\:\:\mid\sqrt{{a}}\:{cos}^{\mathrm{2}} \left({x}\right)+\sqrt{{b}}\:{sin}^{\mathrm{2}} \left({x}\right)\mid\leqslant\sqrt{{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….. \\ $$$$\:\:\:\:\: \\ $$
