Question Number 140966 by mnjuly1970 last updated on 14/May/21
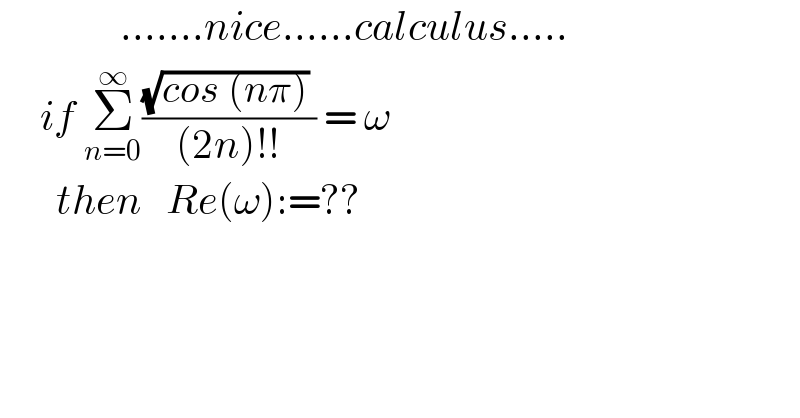
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…….{nice}……{calculus}….. \\ $$$$\:\:\:\:\:{if}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\sqrt{{cos}\:\left({n}\pi\right)}\:}{\left(\mathrm{2}{n}\right)!!}\:=\:\omega \\ $$$$\:\:\:\:\:\:\:{then}\:\:\:{Re}\left(\omega\right):=?? \\ $$
Answered by Dwaipayan Shikari last updated on 14/May/21
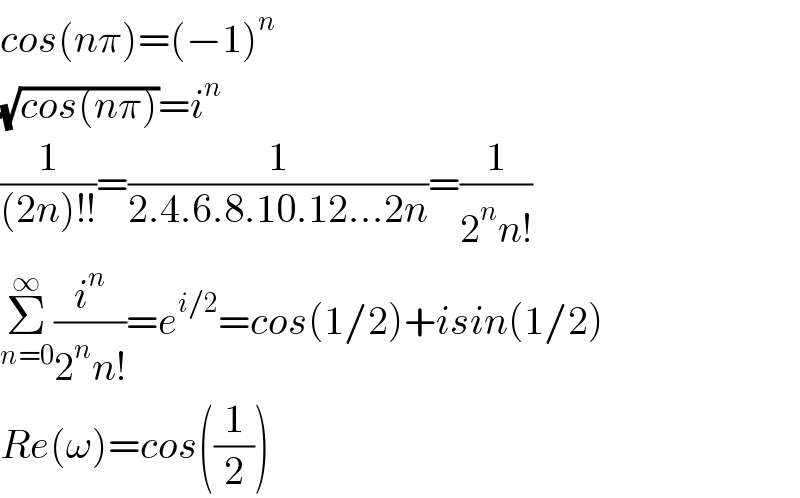
$${cos}\left({n}\pi\right)=\left(−\mathrm{1}\right)^{{n}} \\ $$$$\sqrt{{cos}\left({n}\pi\right)}={i}^{{n}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)!!}=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\mathrm{10}.\mathrm{12}…\mathrm{2}{n}}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}!} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{i}^{{n}} }{\mathrm{2}^{{n}} {n}!}={e}^{{i}/\mathrm{2}} ={cos}\left(\mathrm{1}/\mathrm{2}\right)+{isin}\left(\mathrm{1}/\mathrm{2}\right) \\ $$$${Re}\left(\omega\right)={cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by mnjuly1970 last updated on 14/May/21

$$\:\:\:\:\:{thanks}\:{alot}\:{mr}\:{payan}… \\ $$
