Question Number 141946 by mnjuly1970 last updated on 27/May/21
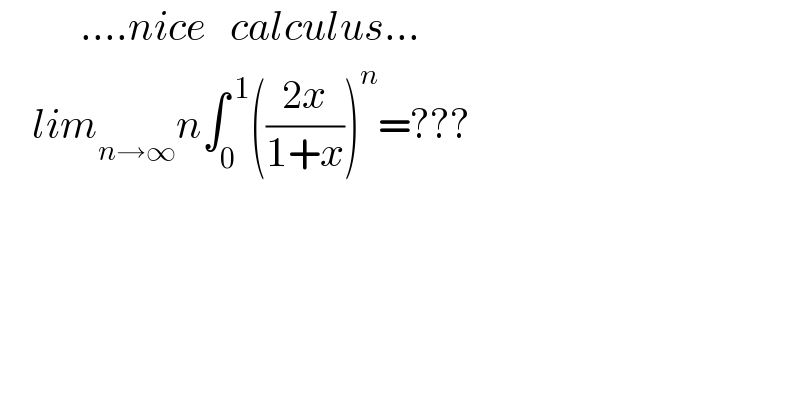
$$\:\:\:\:\:\:\:\:\:\:….{nice}\:\:\:{calculus}… \\ $$$$\:\:\:\:{lim}_{{n}\rightarrow\infty} {n}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}}\right)^{{n}} =??? \\ $$
Answered by mnjuly1970 last updated on 29/May/21
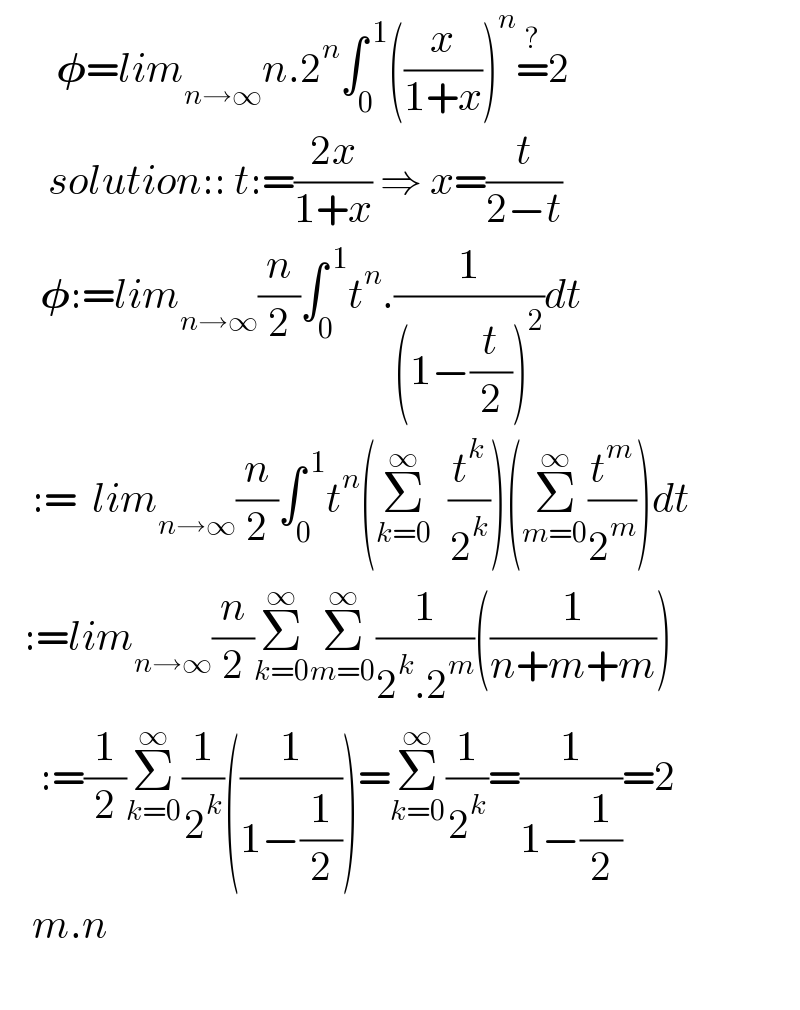
$$\:\:\:\:\:\:\:\boldsymbol{\phi}={lim}_{{n}\rightarrow\infty} {n}.\mathrm{2}^{{n}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{x}}{\mathrm{1}+{x}}\right)^{{n}} \overset{?} {=}\mathrm{2} \\ $$$$\:\:\:\:\:\:{solution}::\:{t}:=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}}\:\Rightarrow\:{x}=\frac{{t}}{\mathrm{2}−{t}} \\ $$$$\:\:\:\:\:\boldsymbol{\phi}:={lim}_{{n}\rightarrow\infty} \frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {t}^{{n}} .\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right)^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\::=\:\:{lim}_{{n}\rightarrow\infty} \frac{{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {t}^{{n}} \left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\:\frac{{t}^{{k}} }{\mathrm{2}^{{k}} }\right)\left(\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{t}^{{m}} }{\mathrm{2}^{{m}} }\right){dt} \\ $$$$\:\:\::={lim}_{{n}\rightarrow\infty} \frac{{n}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} .\mathrm{2}^{{m}} }\left(\frac{\mathrm{1}}{{n}+{m}+{m}}\right) \\ $$$$\:\:\:\:\::=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{2} \\ $$$$\:\:\:\:{m}.{n} \\ $$$$\:\:\:\:\: \\ $$
