Question Number 136570 by mnjuly1970 last updated on 23/Mar/21

$$\:\:\:\:\:\:\:\:\:…….{nice}\:\:…..\:\:\:{calculus}….. \\ $$$$\:\:\:\:\Omega=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}} \left({x}\right).{cos}\left({nx}\right)=? \\ $$$$\:\:\:{solution}:::: \\ $$$$\:\:\:\:\Omega=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}−\mathrm{1}} \left({x}\right)\left\{{cos}\left({x}−{nx}\right)+{cos}\left({x}+{nx}\right)\right. \\ $$$$\:\:\therefore\:\mathrm{2}\Omega=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}−\mathrm{1}} \left({x}\right).{cos}\left({n}−\mathrm{1}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}−\mathrm{1}} \left({x}\right).{cos}\left({n}+\mathrm{1}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{cos}^{{n}−\mathrm{1}} \left({x}\right).{cos}\left({n}−\mathrm{1}\right){x}+\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}+\mathrm{1}} \left({x}\right).{cos}\left({n}+\mathrm{1}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{1}+\Omega+\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}\left(\Omega−\mathrm{1}\right) \\ $$$$\:\:\:\Omega\left(\mathrm{1}−\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}\right)=\mathrm{1}−\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)} \\ $$$$\:\:\:\:\:\therefore\:\:\:\:\:\:\:\:\:\Omega=\mathrm{1}\:…………….. \\ $$$$\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Mar/21
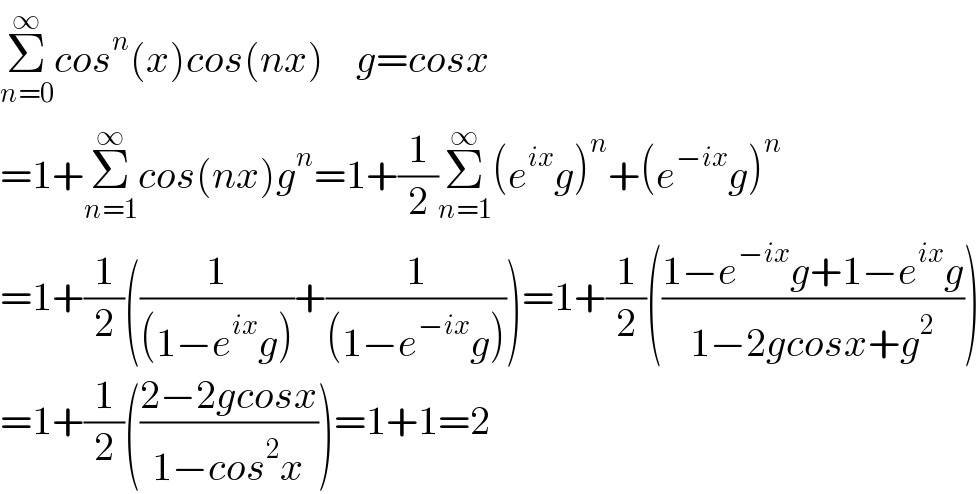
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}^{{n}} \left({x}\right){cos}\left({nx}\right)\:\:\:\:{g}={cosx} \\ $$$$=\mathrm{1}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{cos}\left({nx}\right){g}^{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({e}^{{ix}} {g}\right)^{{n}} +\left({e}^{−{ix}} {g}\right)^{{n}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{e}^{{ix}} {g}\right)}+\frac{\mathrm{1}}{\left(\mathrm{1}−{e}^{−{ix}} {g}\right)}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}−{e}^{−{ix}} {g}+\mathrm{1}−{e}^{{ix}} {g}}{\mathrm{1}−\mathrm{2}{gcosx}+{g}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}−\mathrm{2}{gcosx}}{\mathrm{1}−{cos}^{\mathrm{2}} {x}}\right)=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
