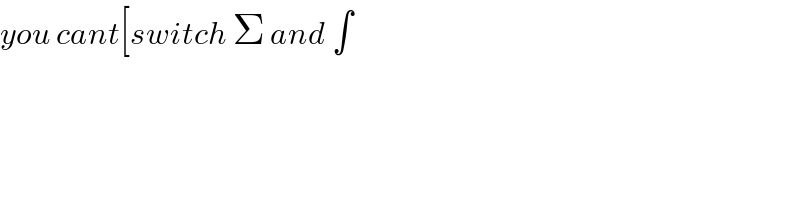Question Number 136295 by mnjuly1970 last updated on 20/Mar/21
$$\:\:\:\:\:\:….{nice}\:\:{calculus}… \\ $$$${prove}\::: \\ $$$$\mathrm{1}\:::\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{tan}^{β\mathrm{1}} \left(\sqrt{{tan}\left({x}\right)}\:\right)}{{tan}\left({x}\right)}{dx}=\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}+\sqrt{\mathrm{2}}\:\right) \\ $$$$\mathrm{2}::\Omega=\int_{β\pi} ^{\:\pi} \frac{{e}^{\left({sin}\left({x}\right)+{cos}\left({x}\right)\right)} {cos}\left({sin}\left({x}\right)\right)}{{e}^{{x}} +{e}^{{sin}\left({x}\right)} }{dx}=\pi \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
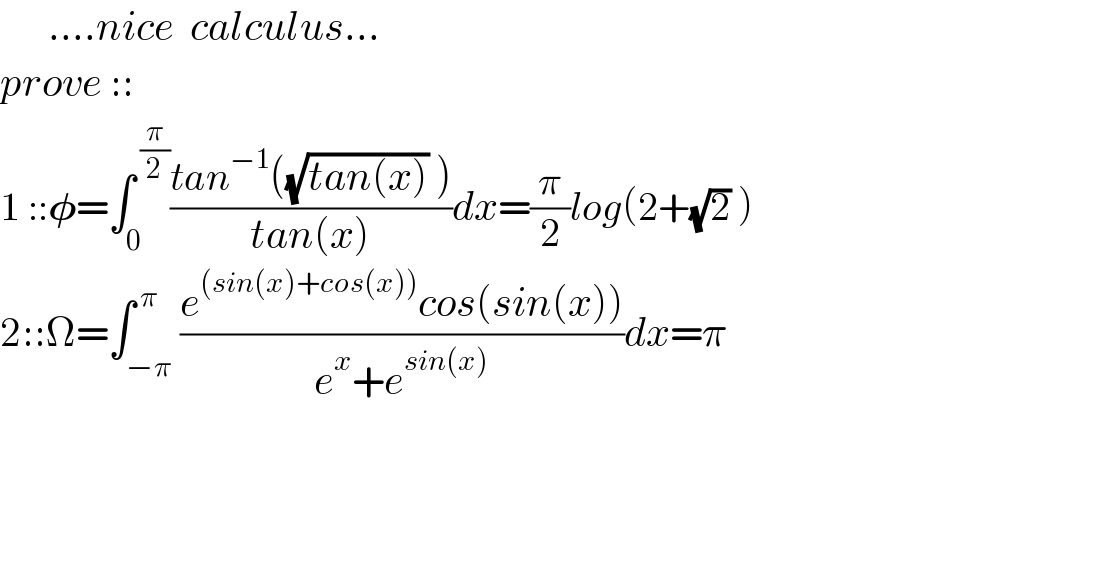
Answered by mindispower last updated on 20/Mar/21
![Ξ©=Reβ«_(βΟ) ^Ο (e^(cos(x)+sin(x)(+isin(x)) /(e^x +sin(x)))dx=Re(W) W=β«_(βΟ) ^Ο (e^(cos(x)+isin(x)) /(e^(xβsin(x)) +1))dx,z=cos(x)+isin(x),z^β ,conj(z) by semetry xββx 2w=β«_(βΟ) ^Ο (e^z^β /(e^(βx+sin(x)) +1))+(e^z /(e^(xβsin(x)) +1))dx =β«_(βΟ) ^Ο ((e^z^β (e^(xβsin(x)) )+e^z )/(e^(xβsin(x)) +1))dx =β«_(βΟ) ^Ο e^z^β +β«_(βΟ) ^Ο ((e^z βe^z^β )/(e^(xβsin(x)) +1))dx 2w=A+B Bβ{ia,aβR} Ξ©=Re(w)=(1/2)Reβ«_(βΟ) ^Ο e^z^β dx,xββx,sin(βx)=βsin(x)β =(1/2)Reβ«_(βΟ) ^Ο e^z dx=(1/2)ReΞ£_(nβ₯0) β«_(βΟ) ^Ο (z^n /(n!))dx z=e^(ix) βΞ©=(1/2).ReΞ£_(nβ₯0) β«_(βΟ) ^Ο (e^(inx) /(n!))dx=(1/2)β«_(βΟ) ^Ο dx_(=C) +Ξ£_(nβ₯1) [_(βΟ) ^Ο (e^(inx) /(n!.n))]_(=D) xβe^(inx) is 2Ο periodicβD=0 Ξ©=(1/2).2Ο+0=Ο β«_(βΟ) ^Ο ((e^(cos(x)+sin(x)) cos(sin(x))/(e^x +e^(sin(x)) ))dx=π](https://www.tinkutara.com/question/Q136297.png)
$$\Omega={Re}\int_{β\pi} ^{\pi} \frac{{e}^{{cos}\left({x}\right)+{sin}\left({x}\right)\left(+{isin}\left({x}\right)\right.} }{{e}^{{x}} +{sin}\left({x}\right)}{dx}={Re}\left({W}\right) \\ $$$${W}=\int_{β\pi} ^{\pi} \frac{{e}^{{cos}\left({x}\right)+{isin}\left({x}\right)} }{{e}^{{x}β{sin}\left({x}\right)} +\mathrm{1}}{dx},{z}={cos}\left({x}\right)+{isin}\left({x}\right),\overset{β} {{z}},{conj}\left({z}\right) \\ $$$${by}\:{semetry}\:\:{x}\rightarrowβ{x} \\ $$$$\mathrm{2}{w}=\int_{β\pi} ^{\pi} \frac{{e}^{\overset{β} {{z}}} }{{e}^{β{x}+{sin}\left({x}\right)} +\mathrm{1}}+\frac{{e}^{{z}} }{{e}^{{x}β{sin}\left({x}\right)} +\mathrm{1}}{dx} \\ $$$$=\int_{β\pi} ^{\pi} \frac{{e}^{\overset{β} {{z}}} \left({e}^{{x}β{sin}\left({x}\right)} \right)+{e}^{{z}} }{{e}^{{x}β{sin}\left({x}\right)} +\mathrm{1}}{dx} \\ $$$$=\int_{β\pi} ^{\pi} {e}^{\overset{β} {{z}}} +\int_{β\pi} ^{\pi} \frac{{e}^{{z}} β{e}^{\overset{β} {{z}}} }{{e}^{{x}β{sin}\left({x}\right)} +\mathrm{1}}{dx} \\ $$$$\mathrm{2}{w}={A}+{B} \\ $$$${B}\in\left\{{ia},{a}\in\mathbb{R}\right\} \\ $$$$\Omega={Re}\left({w}\right)=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{β\pi} ^{\pi} {e}^{\overset{β} {{z}}} {dx},{x}\rightarrowβ{x},{sin}\left(β{x}\right)=β{sin}\left({x}\right)\Rightarrow \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{β\pi} ^{\pi} {e}^{{z}} {dx}=\frac{\mathrm{1}}{\mathrm{2}}{Re}\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{β\pi} ^{\pi} \frac{{z}^{{n}} }{{n}!}{dx} \\ $$$${z}={e}^{{ix}} \\ $$$$\Leftrightarrow\Omega=\frac{\mathrm{1}}{\mathrm{2}}.{Re}\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{β\pi} ^{\pi} \frac{{e}^{{inx}} }{{n}!}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{β\pi} ^{\pi} {d}\underset{={C}} {{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left[_{β\pi} ^{\pi} \frac{{e}^{{inx}} }{{n}!.{n}}\underset{={D}} {\right]} \\ $$$${x}\rightarrow{e}^{{inx}} {is}\:\mathrm{2}\pi\:{periodic}\Rightarrow{D}=\mathrm{0} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}\pi+\mathrm{0}=\pi \\ $$$$\int_{β\pi} ^{\pi} \frac{{e}^{{cos}\left({x}\right)+{sin}\left({x}\right)} {cos}\left({sin}\left({x}\right)\right.}{{e}^{{x}} +{e}^{{sin}\left({x}\right)} }{dx}=\boldsymbol{\pi} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 20/Mar/21
$${very}\:{nice}\:{solution} \\ $$$${thanks}\:{alot}… \\ $$
Commented by mindispower last updated on 20/Mar/21
$${thanx}\:{always}\:{pleasur} \\ $$
Answered by Ar Brandon last updated on 20/Mar/21
$$\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{tan}^{β\mathrm{1}} \left(\sqrt{\mathrm{tanx}}\right)}{\mathrm{tanx}}\mathrm{dx}\underset{\mathrm{u}=\mathrm{tanx}} {=}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{β\mathrm{1}} \left(\sqrt{\mathrm{u}}\right)}{\mathrm{u}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\mathrm{n}} }{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$\:\:\:\:\:\underset{\mathrm{t}=\mathrm{u}^{\mathrm{2}} } {=}\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{n}}{\mathrm{2}}β\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\mathrm{t}\right)}\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\beta\left(\frac{\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\:,\:\frac{\mathrm{1}}{\mathrm{2}}β\frac{\mathrm{n}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(β\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\centerdot\frac{\pi}{\mathrm{cos}\left(\frac{\pi\mathrm{n}}{\mathrm{2}}\right)} \\ $$π·
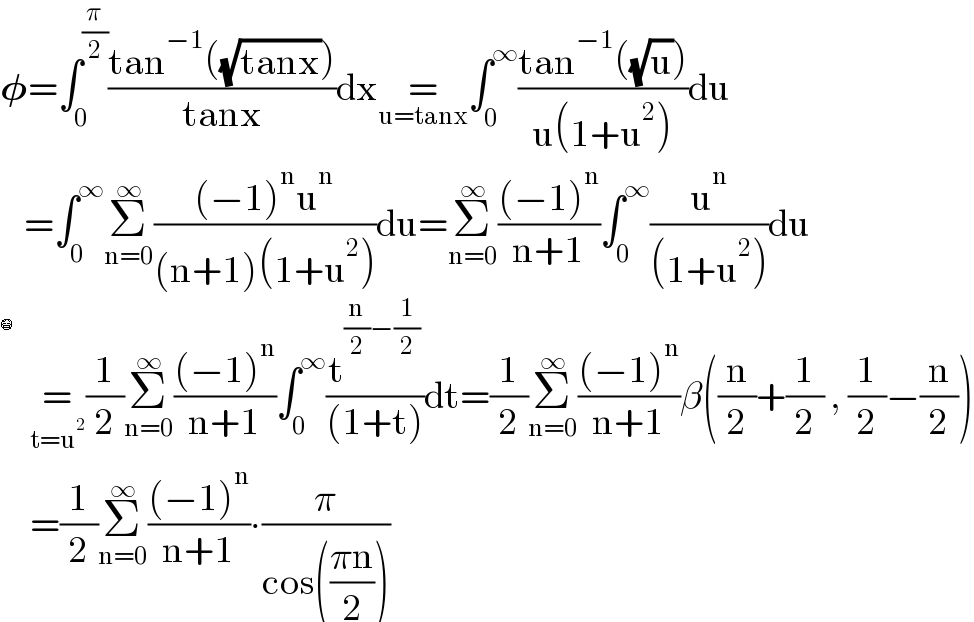
Commented by mindispower last updated on 20/Mar/21
$${you}\:{cant}\left[{switch}\:\Sigma\:{and}\:\int\right. \\ $$