Question Number 138065 by mnjuly1970 last updated on 09/Apr/21
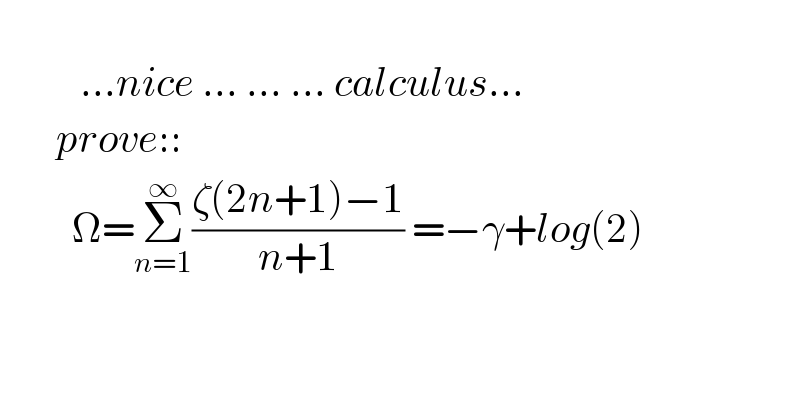
$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:…{nice}\:…\:…\:…\:{calculus}… \\ $$$$\:\:\:\:\:\:\:{prove}:: \\ $$$$\:\:\:\:\:\:\:\:\:\Omega=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\zeta\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{1}}{{n}+\mathrm{1}}\:=−\gamma+{log}\left(\mathrm{2}\right) \\ $$
Answered by Ñï= last updated on 09/Apr/21
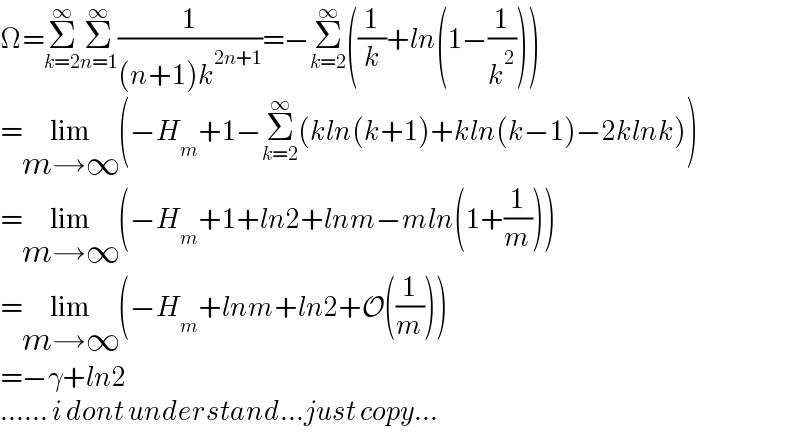
$$\Omega=\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right){k}^{\mathrm{2}{n}+\mathrm{1}} }=−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}}+{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)\right) \\ $$$$=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(−{H}_{{m}} +\mathrm{1}−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\left({kln}\left({k}+\mathrm{1}\right)+{kln}\left({k}−\mathrm{1}\right)−\mathrm{2}{klnk}\right)\right) \\ $$$$=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(−{H}_{{m}} +\mathrm{1}+{ln}\mathrm{2}+{lnm}−{mln}\left(\mathrm{1}+\frac{\mathrm{1}}{{m}}\right)\right) \\ $$$$=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(−{H}_{{m}} +{lnm}+{ln}\mathrm{2}+\mathcal{O}\left(\frac{\mathrm{1}}{{m}}\right)\right) \\ $$$$=−\gamma+{ln}\mathrm{2} \\ $$$$……\:{i}\:{dont}\:{understand}…{just}\:{copy}… \\ $$
Commented by mnjuly1970 last updated on 10/Apr/21

Commented by mnjuly1970 last updated on 10/Apr/21

