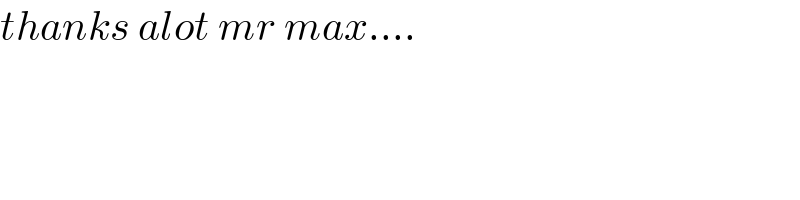nice-calculus-prove-that-0-1-ln-x-1-x-2-x-dx-pi-2-16-

Question Number 137439 by mnjuly1970 last updated on 02/Apr/21

\dots \dots n i c e c a l c u l u s \dots . .

p r o v e t h a t ::

χ = \int_{0}^{1} \frac{l n (x + \sqrt{1 - x^{2}})}{x} d x = \frac{π^{2}}{16} \dots .

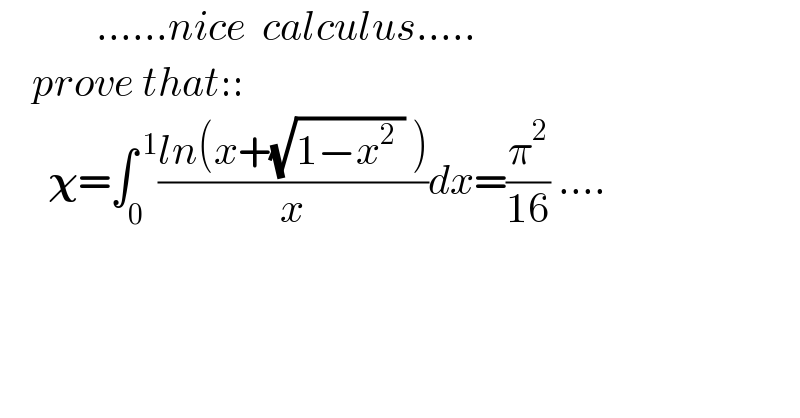
Answered by mindispower last updated on 03/Apr/21

f (t) = \int_{0}^{1} \frac{l n (t x + \sqrt{1 - x^{2}})}{x} d x, W e w a n t f (1)

f^{'} (t) = \int_{0}^{1} \frac{d x}{t x + \sqrt{1 - x^{2}}}

x = s i n (r)

f^{'} (t) = \int_{0}^{\frac{π}{2}} \frac{c o s (r) d r}{t s i n (r) + c o s (r)}

c o s (r) = a (t s i n (r) + c o s (r)) + b (t c o s (r) - s i n (r))

a t - b = 0

a + b t = 1

b = \frac{t}{t^{2} + 1}

a = \frac{1}{1 + t^{2}}

f^{'} (t) = \int_{0}^{\frac{π}{2}} \frac{d r}{1 + t^{2}} + \frac{t}{1 + t^{2}} \int_{0}^{\frac{π}{2}} \frac{t c o s (r) - s i n (r)}{t s i n (r) + c o s (r)} d r

= \frac{π}{2} . \frac{1}{1 + t^{2}} + \frac{t}{1 + t^{2}} l n (t)

f (0) = \frac{1}{2} \int_{0}^{1} \frac{l n (1 - t^{2})}{t} d t = \frac{1}{2} . - \sum_{n ⩾ 0} \int_{0}^{1} \frac{t^{2 n + 1}}{n + 1}

= - \frac{1}{4} \sum_{n ⩾ 0} \frac{1}{{(n + 1)}^{2}} = - \frac{π^{2}}{24}

\int_{0}^{1} f^{'} (t) = f (1) - f (0) = \frac{π}{2} a r c t a n (1) + \int_{0}^{1} \frac{t l n (t)}{1 + t^{2}} d t

= \frac{π^{2}}{8} - \sum_{n ⩾ 0} \frac{{(- 1)}^{n}}{{(2 n + 2)}^{2}} = \frac{π^{2}}{8} - \frac{1}{4} (\frac{π^{2}}{12}) = \frac{5 π^{2}}{48}

f (1) = \frac{5 π^{2}}{48} + f (0) = \frac{5 π^{2}}{48} - \frac{π^{2}}{24} = \frac{π^{2}}{16}

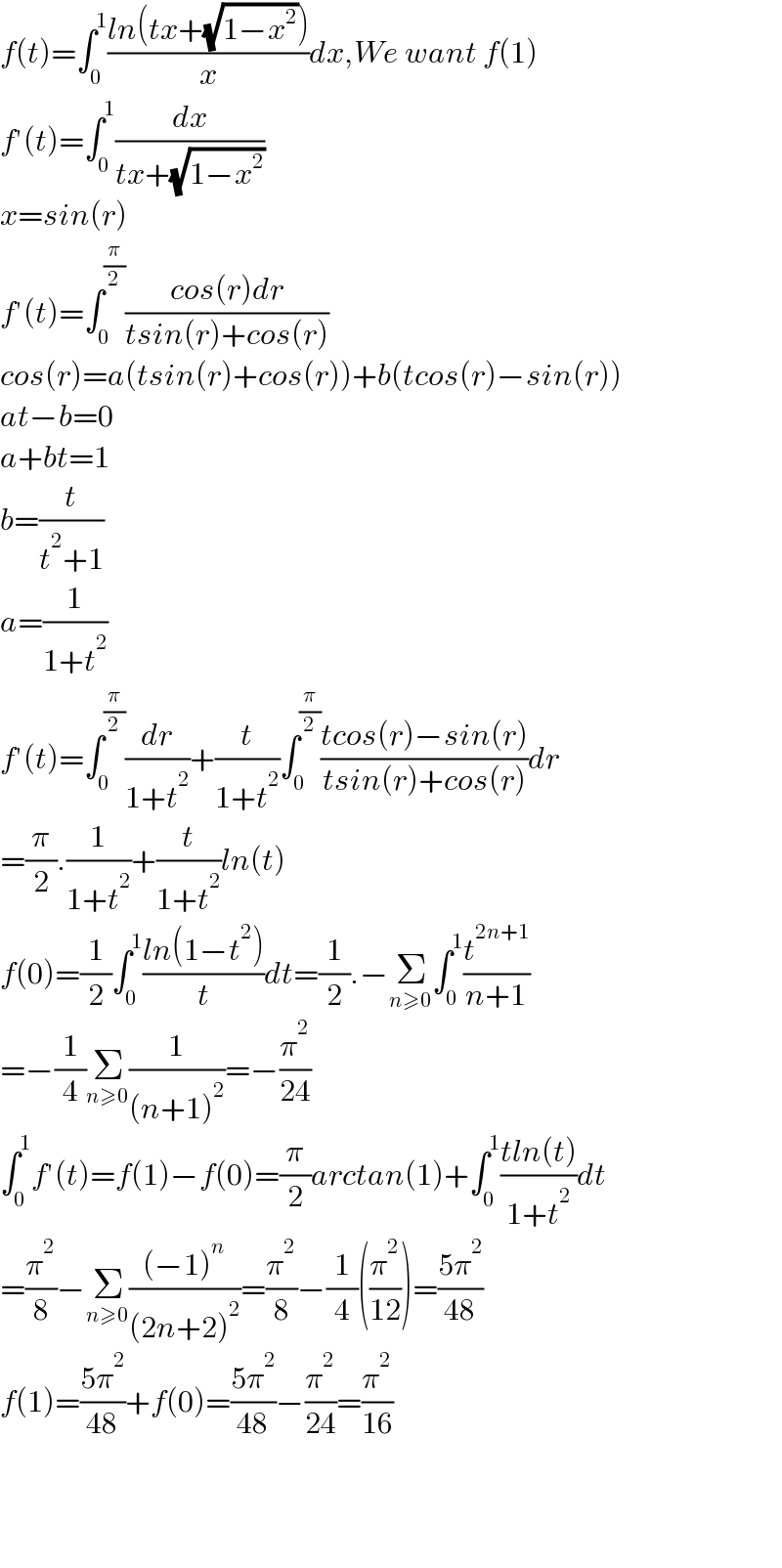
Commented by mnjuly1970 last updated on 03/Apr/21

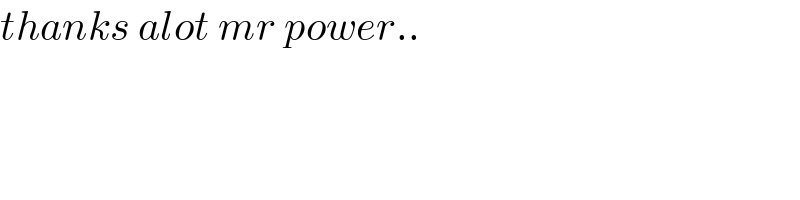
t h a n k s a l o t m r p o w e r . .

Commented by mnjuly1970 last updated on 03/Apr/21

Commented by mindispower last updated on 03/Apr/21

p l e a s u r s i r

Answered by mathmax by abdo last updated on 03/Apr/21

χ = \int_{0}^{1} \frac{\log (x + \sqrt{1 - x^{2}})}{x} dx let f (a) = \int_{0}^{1} \frac{\log (ax + \sqrt{1 - x^{2}})}{x} dx witha > 0

f^{^{'}} (a) = \int_{0}^{1} \frac{x}{x (ax + \sqrt{1 - x^{2}})} dx = \int_{0}^{1} \frac{dx}{ax + \sqrt{1 - x^{2}}}

=_{x = sint} \int_{0}^{\frac{π}{2}} \frac{cost}{asint + cost} dt = \int_{0}^{\frac{π}{2}} \frac{dt}{atant + 1}

=_{tant = y} \int_{0}^{\infty} \frac{1}{ay + 1} \times \frac{dy}{(1 + y^{2})} let decompose

F (y) = \frac{1}{(ay + 1) (y^{2} + 1)} \Rightarrow F (y) = \frac{α}{ay + 1} + \frac{β y + δ}{y^{2} + 1}

α = \frac{1}{\frac{1}{a^{2}} + 1} = \frac{a^{2}}{a^{2} + 1}

\lim_{y \to + \infty} yF (y) = 0 = \frac{α}{a} + β \Rightarrow β = - \frac{a}{a^{2} + 1}

F (0) = 1 = α + δ \Rightarrow δ = 1 - \frac{a^{2}}{a^{2} + 1} = \frac{1}{a^{2} + 1} \Rightarrow

F (y) = \frac{a^{2}}{(a^{2} + 1) (ay + 1)} + \frac{- \frac{a}{1 + a^{2}} y + \frac{1}{1 + a^{2}}}{y^{2} + 1} \Rightarrow

\int_{0}^{\infty} F (y) dy = \frac{1}{a^{2} + 1} \int_{0}^{\infty} (\frac{a^{2} dy}{ay + 1} - \frac{ay - 1}{y^{2} + 1}) dy

= \frac{1}{a^{2} + 1} \int_{0}^{\infty} (\frac{a^{2}}{ay + 1} - \frac{a}{2} \frac{2 y}{y^{2} + 1} + \frac{1}{y^{2} + 1}) dy

= \frac{1}{a^{2} + 1} {[aln (ay + 1) - aln \sqrt{y^{2} + 1}]}_{0}^{\infty} + \frac{π}{2 (1 + a^{2})}

= \frac{a}{a^{2} + 1} {[\ln (\frac{ay + 1}{\sqrt{y^{2} + 1}})]}_{0}^{\infty} + \frac{π}{2 (1 + a^{2})}

= \frac{aloga}{a^{2} + 1} + \frac{π}{2 (a^{2} + 1)} = f^{^{'}} (a) \Rightarrow

f (a) = \int \frac{aloga}{a^{2} + 1} da + \frac{π}{2} \arctan (a) + C

f (1) - f (0) = \int_{0}^{1} f^{^{'}} (a) da = \int_{0}^{1} \frac{aloga}{1 + a^{2}} da + \frac{π}{2} \int_{0}^{1} \frac{da}{1 + a^{2}}

\int_{0}^{1} \frac{da}{1 + a^{2}} = {[arctana]}_{0}^{1} = \frac{π}{4}

\int_{0}^{1} \frac{aloga}{1 + a^{2}} da = {[\frac{1}{2} \log (1 + a^{2}) loga]}_{0}^{1} - \frac{1}{2} \int_{0}^{1} \frac{\log (1 + a^{2})}{a} da

= - \frac{1}{2} \int_{0}^{1} \frac{\log (1 + a^{2})}{a} da

(\log {(1 + u)}^{^{'}} = \frac{1}{1 + u} = \sum_{n = 0}^{\infty} {(- 1)}^{n} u^{n} \Rightarrow \log (1 + u) = \sum_{n = 0}^{\infty} {(- 1)}^{n} \frac{u^{n + 1}}{n + 1}

= \sum_{n = 1}^{\infty} {(- 1)}^{n - 1} \frac{u^{n}}{n} \Rightarrow \log (1 + x^{2}) = \sum_{n = 1}^{\infty} {(- 1)}^{n - 1} \frac{x^{2 n}}{n} \Rightarrow

\int_{0}^{1} \frac{\log (1 + x^{2})}{x} dx = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (2 n + 1)} = u_{n}

\frac{u_{n}}{2} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{2 n (2 n + 1)} = \sum_{n = 1}^{\infty} {(- 1)}^{n - 1} (\frac{1}{2 n} - \frac{1}{2 n + 1})

= \frac{1}{2} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{2 n + 1}

= \frac{\log 2}{2} - (\frac{π}{4} - 1) \Rightarrow f (1) - f (0) = - \frac{\log 2}{4} + \frac{1}{2} (\frac{π}{4} - 1)

= - \frac{\log 2}{4} + \frac{π}{8} - \frac{1}{2} \Rightarrow f (1) = χ = - \frac{\log 2}{4} + \frac{π}{8} - \frac{1}{2} + f (0)

f (0) = \int_{0}^{1} \frac{\log (\sqrt{1 - x^{2}})}{x} dx rest to find f (0) \dots . be continued \dots

Commented by mnjuly1970 last updated on 03/Apr/21

t h a n k s a l o t m r m a x \dots .