Question Number 138163 by mnjuly1970 last updated on 10/Apr/21
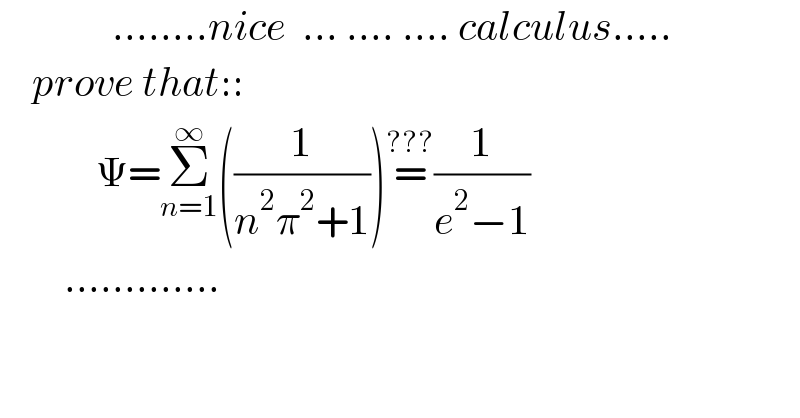
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..{nice}\:\:…\:….\:….\:{calculus}….. \\ $$$$\:\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Psi=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} \pi^{\mathrm{2}} +\mathrm{1}}\right)\overset{???} {=}\frac{\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:…………. \\ $$
Answered by Dwaipayan Shikari last updated on 10/Apr/21
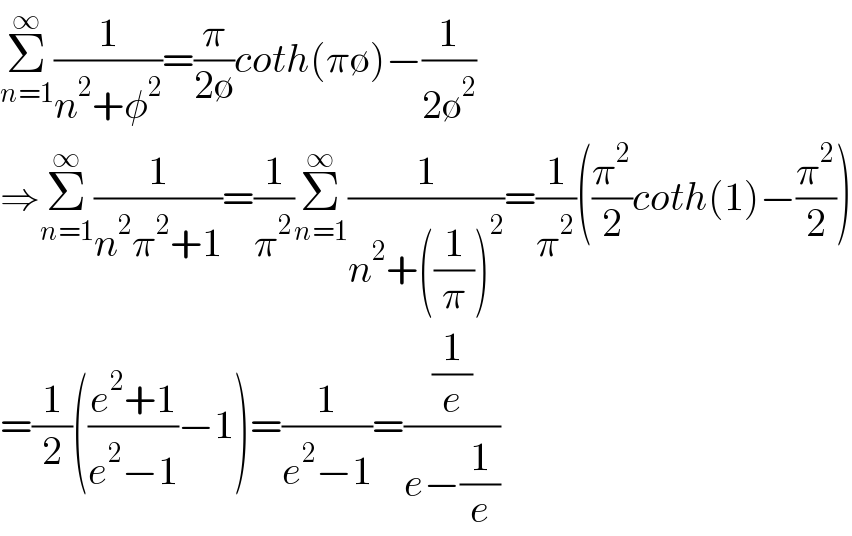
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\phi^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}\emptyset}{coth}\left(\pi\emptyset\right)−\frac{\mathrm{1}}{\mathrm{2}\emptyset^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \pi^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\pi}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\left(\frac{\pi^{\mathrm{2}} }{\mathrm{2}}{coth}\left(\mathrm{1}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{e}^{\mathrm{2}} +\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\right)=\frac{\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}}=\frac{\frac{\mathrm{1}}{{e}}}{{e}−\frac{\mathrm{1}}{{e}}} \\ $$
Commented by mnjuly1970 last updated on 10/Apr/21

$$\:\:\:\:{greateful}..{mr}..{payan}… \\ $$
