Menu Close

nice-calculus-prove-that-n-1-1-n-ln-n-n-ln-2-1-2-ln-2-2-

Tinku Tara 0 Comments
Pin




Question Number 132519 by mnjuly1970 last updated on 14/Feb/21
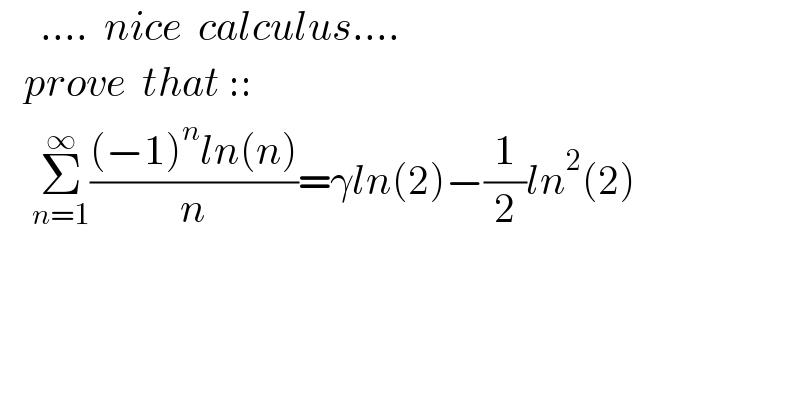
.... nice calculus.... prove that :: Σ_(n=1) ^∞ (((−1)^n ln(n))/n)=γln(2)−(1/2)ln^2 (2)
$$\:\:\:\:\:….\:\:{nice}\:\:{calculus}…. \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {ln}\left({n}\right)}{{n}}=\gamma{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$ \\ $$
Answered by mindispower last updated on 15/Feb/21
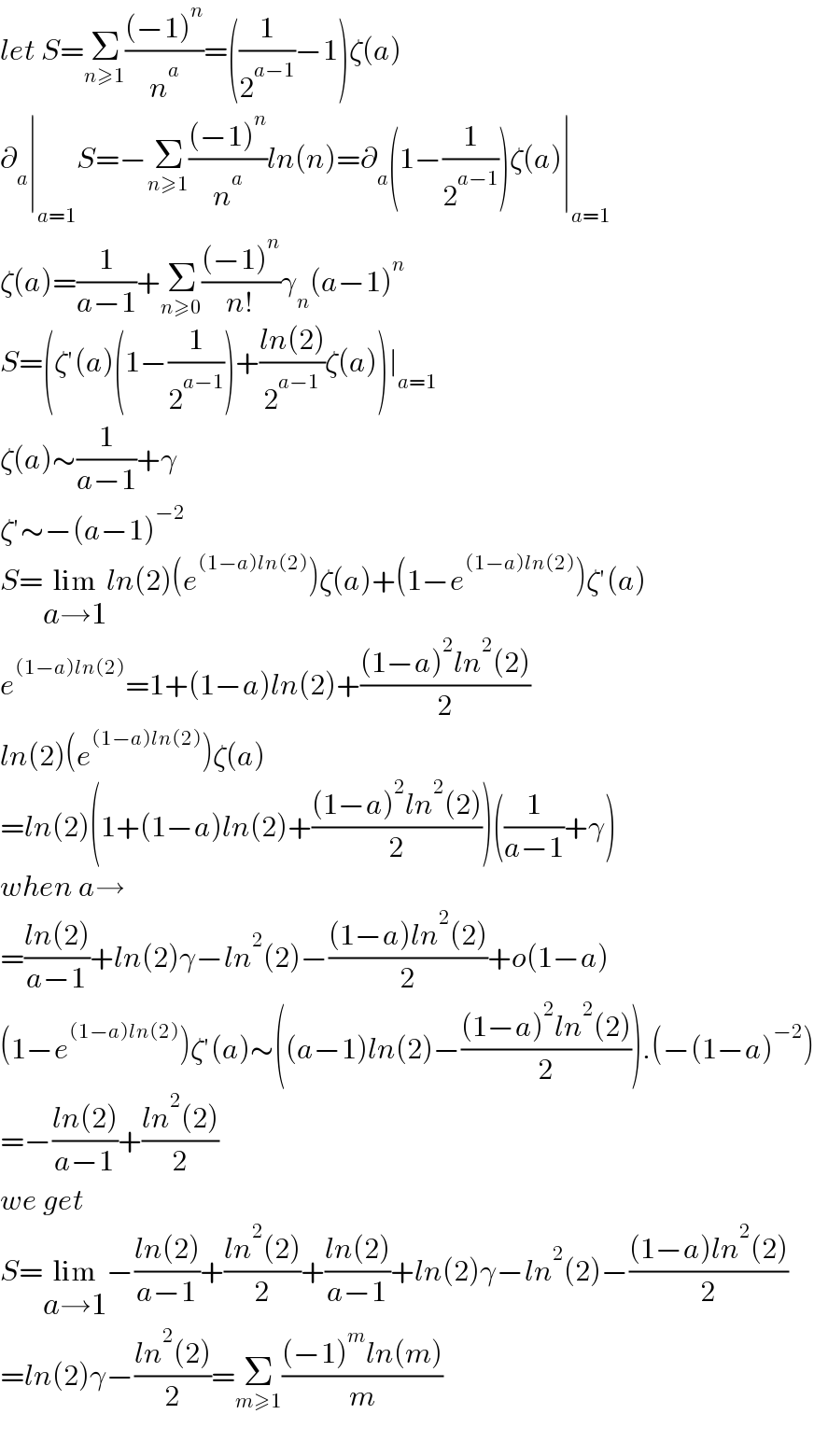
let S=Σ_(n≥1) (((−1)^n )/n^a )=((1/2^(a−1) )−1)ζ(a) ∂_a ∣_(a=1) S=−Σ_(n≥1) (((−1)^n )/n^a )ln(n)=∂_a (1−(1/2^(a−1) ))ζ(a)∣_(a=1) ζ(a)=(1/(a−1))+Σ_(n≥0) (((−1)^n )/(n!))γ_n (a−1)^n S=(ζ′(a)(1−(1/2^(a−1) ))+((ln(2))/2^(a−1) )ζ(a))∣_(a=1) ζ(a)∼(1/(a−1))+γ ζ′∼−(a−1)^(−2) S=lim_(a→1) ln(2)(e^((1−a)ln(2)) )ζ(a)+(1−e^((1−a)ln(2)) )ζ′(a) e^((1−a)ln(2)) =1+(1−a)ln(2)+(((1−a)^2 ln^2 (2))/2) ln(2)(e^((1−a)ln(2)) )ζ(a) =ln(2)(1+(1−a)ln(2)+(((1−a)^2 ln^2 (2))/2))((1/(a−1))+γ) when a→ =((ln(2))/(a−1))+ln(2)γ−ln^2 (2)−(((1−a)ln^2 (2))/2)+o(1−a) (1−e^((1−a)ln(2)) )ζ′(a)∼((a−1)ln(2)−(((1−a)^2 ln^2 (2))/2)).(−(1−a)^(−2) ) =−((ln(2))/(a−1))+((ln^2 (2))/2) we get S=lim_(a→1) −((ln(2))/(a−1))+((ln^2 (2))/2)+((ln(2))/(a−1))+ln(2)γ−ln^2 (2)−(((1−a)ln^2 (2))/2) =ln(2)γ−((ln^2 (2))/2)=Σ_(m≥1) (((−1)^m ln(m))/m)
$${let}\:{S}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{a}} }=\left(\frac{\mathrm{1}}{\mathrm{2}^{{a}−\mathrm{1}} }−\mathrm{1}\right)\zeta\left({a}\right) \\ $$$$\partial_{{a}} \mid_{{a}=\mathrm{1}} {S}=−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{a}} }{ln}\left({n}\right)=\partial_{{a}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{a}−\mathrm{1}} }\right)\zeta\left({a}\right)\mid_{{a}=\mathrm{1}} \\ $$$$\zeta\left({a}\right)=\frac{\mathrm{1}}{{a}−\mathrm{1}}+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\gamma_{{n}} \left({a}−\mathrm{1}\right)^{{n}} \\ $$$${S}=\left(\zeta'\left({a}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{a}−\mathrm{1}} }\right)+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}^{{a}−\mathrm{1}} }\zeta\left({a}\right)\right)\mid_{{a}=\mathrm{1}} \\ $$$$\zeta\left({a}\right)\sim\frac{\mathrm{1}}{{a}−\mathrm{1}}+\gamma \\ $$$$\zeta'\sim−\left({a}−\mathrm{1}\right)^{−\mathrm{2}} \\ $$$${S}=\underset{{a}\rightarrow\mathrm{1}} {\mathrm{lim}}{ln}\left(\mathrm{2}\right)\left({e}^{\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)} \right)\zeta\left({a}\right)+\left(\mathrm{1}−{e}^{\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)} \right)\zeta'\left({a}\right) \\ $$$${e}^{\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)} =\mathrm{1}+\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)+\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${ln}\left(\mathrm{2}\right)\left({e}^{\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)} \right)\zeta\left({a}\right) \\ $$$$={ln}\left(\mathrm{2}\right)\left(\mathrm{1}+\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)+\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{{a}−\mathrm{1}}+\gamma\right) \\ $$$${when}\:{a}\rightarrow \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{{a}−\mathrm{1}}+{ln}\left(\mathrm{2}\right)\gamma−{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\left(\mathrm{1}−{a}\right){ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+{o}\left(\mathrm{1}−{a}\right) \\ $$$$\left(\mathrm{1}−{e}^{\left(\mathrm{1}−{a}\right){ln}\left(\mathrm{2}\right)} \right)\zeta'\left({a}\right)\sim\left(\left({a}−\mathrm{1}\right){ln}\left(\mathrm{2}\right)−\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{2}} {ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\right).\left(−\left(\mathrm{1}−{a}\right)^{−\mathrm{2}} \right) \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)}{{a}−\mathrm{1}}+\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${we}\:{get} \\ $$$${S}=\underset{{a}\rightarrow\mathrm{1}} {\mathrm{lim}}−\frac{{ln}\left(\mathrm{2}\right)}{{a}−\mathrm{1}}+\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\frac{{ln}\left(\mathrm{2}\right)}{{a}−\mathrm{1}}+{ln}\left(\mathrm{2}\right)\gamma−{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\left(\mathrm{1}−{a}\right){ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$={ln}\left(\mathrm{2}\right)\gamma−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{m}} {ln}\left({m}\right)}{{m}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 15/Feb/21
thanks alot sir power..
$${thanks}\:{alot}\:{sir}\:{power}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *