Question Number 141057 by mnjuly1970 last updated on 15/May/21
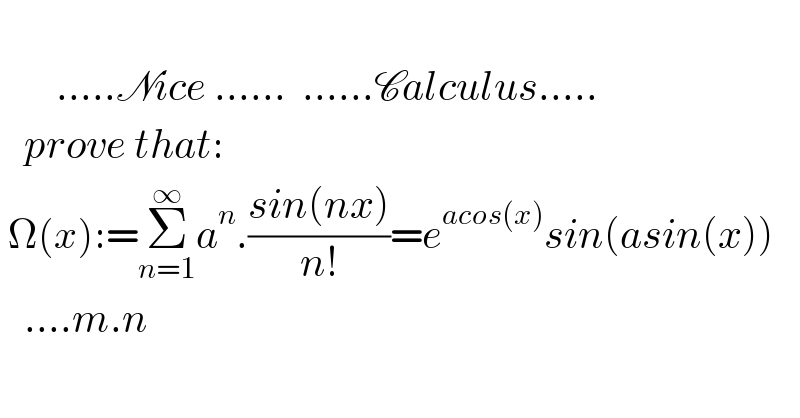
$$ \\ $$$$\:\:\:\:\:\:\:…..\mathscr{N}{ice}\:……\:\:……\mathscr{C}{alculus}….. \\ $$$$\:\:\:{prove}\:{that}: \\ $$$$\:\Omega\left({x}\right):=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{a}^{{n}} .\frac{{sin}\left({nx}\right)}{{n}!}={e}^{{acos}\left({x}\right)} {sin}\left({asin}\left({x}\right)\right) \\ $$$$\:\:\:….{m}.{n} \\ $$
Answered by Dwaipayan Shikari last updated on 15/May/21
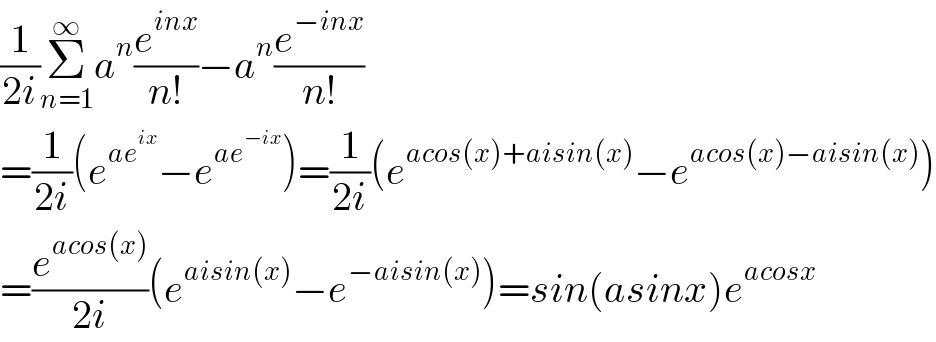
$$\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{a}^{{n}} \frac{{e}^{{inx}} }{{n}!}−{a}^{{n}} \frac{{e}^{−{inx}} }{{n}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left({e}^{{ae}^{{ix}} } −{e}^{{ae}^{−{ix}} } \right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left({e}^{{acos}\left({x}\right)+{aisin}\left({x}\right)} −{e}^{{acos}\left({x}\right)−{aisin}\left({x}\right)} \right) \\ $$$$=\frac{{e}^{{acos}\left({x}\right)} }{\mathrm{2}{i}}\left({e}^{{aisin}\left({x}\right)} −{e}^{−{aisin}\left({x}\right)} \right)={sin}\left({asinx}\right){e}^{{acosx}} \\ $$
Commented by mnjuly1970 last updated on 15/May/21

$${thanks}\:{alot}.. \\ $$
Commented by Dwaipayan Shikari last updated on 15/May/21

$$\left.:−\right) \\ $$
Answered by mindispower last updated on 15/May/21
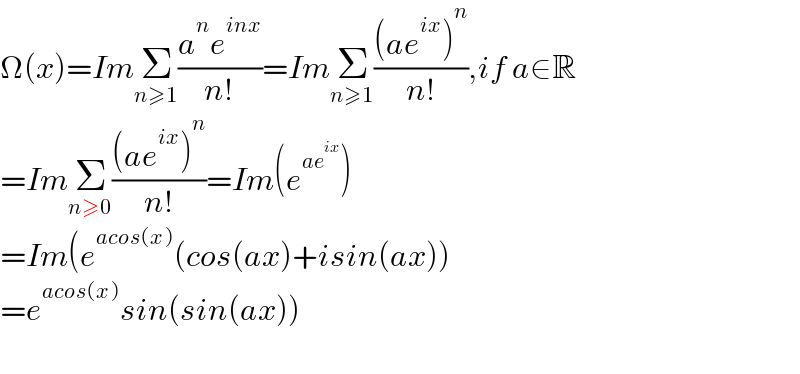
$$\Omega\left({x}\right)={Im}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{a}^{{n}} {e}^{{inx}} }{{n}!}={Im}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left({ae}^{{ix}} \right)^{{n}} }{{n}!},{if}\:{a}\in\mathbb{R} \\ $$$$={Im}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left({ae}^{{ix}} \right)^{{n}} }{{n}!}={Im}\left({e}^{{ae}^{{ix}} } \right) \\ $$$$={Im}\left({e}^{{acos}\left({x}\right)} \left({cos}\left({ax}\right)+{isin}\left({ax}\right)\right)\right. \\ $$$$={e}^{{acos}\left({x}\right)} {sin}\left({sin}\left({ax}\right)\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 15/May/21

$${grateful}.. \\ $$
Commented by mindispower last updated on 15/May/21

$${pleasur} \\ $$
