Menu Close

nice-integral-0-1-li-2-1-x-2-x-dx-m-n-

Tinku Tara 0 Comments
Pin




Question Number 142773 by mnjuly1970 last updated on 05/Jun/21
.......nice ......integral...... 𝛗:=∫_(0 ) ^( 1) ((li_2 (1βˆ’x))/(2βˆ’x)) dx=?? .......m.n...
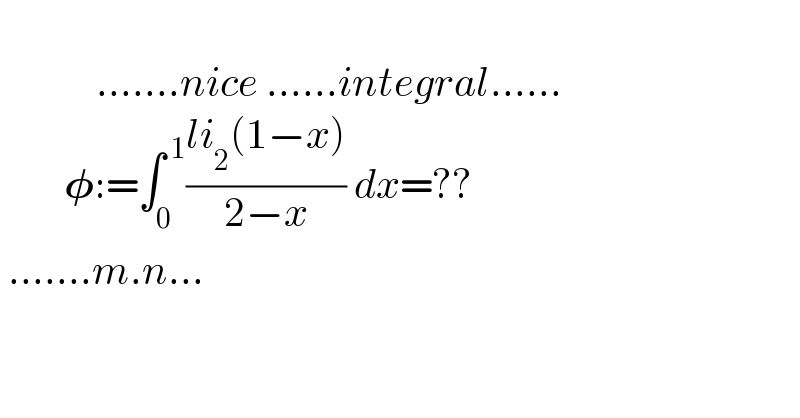
$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…….{nice}\:……{integral}…… \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}:=\int_{\mathrm{0}\:} ^{\:\mathrm{1}} \frac{{li}_{\mathrm{2}} \left(\mathrm{1}βˆ’{x}\right)}{\mathrm{2}βˆ’{x}}\:{dx}=?? \\ $$$$\:…….{m}.{n}… \\ $$
Answered by mnjuly1970 last updated on 05/Jun/21
𝛗:=∫_0 ^( 1) ((li_2 (x))/(1+x))dx=[li_2 (x).ln(1+x)]_0 ^1 +∫_0 ^( 1) ((ln(1βˆ’x).ln(1+x))/x)dx = (Ο€^2 /6)ln(2)βˆ’(5/8) ΞΆ(3)... derived earlier: ∫_0 ^( 1) ((ln(1βˆ’x)ln(1+x))/x)dx=((βˆ’5)/8) ΞΆ(3)
$$\:\:\:\boldsymbol{\phi}:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{li}_{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}=\left[{li}_{\mathrm{2}} \left({x}\right).{ln}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}βˆ’{x}\right).{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$$$=\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}{ln}\left(\mathrm{2}\right)βˆ’\frac{\mathrm{5}}{\mathrm{8}}\:\zeta\left(\mathrm{3}\right)… \\ $$$$\:{derived}\:\:{earlier}: \\ $$$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}βˆ’{x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}=\frac{βˆ’\mathrm{5}}{\mathrm{8}}\:\zeta\left(\mathrm{3}\right) \\ $$$$\: \\ $$$$ \\ $$
Answered by qaz last updated on 05/Jun/21
Ο†=∫_0 ^1 ((Li_2 (1βˆ’x))/(2βˆ’x))dx=∫_0 ^1 ((Li_2 (x))/(1+x))dx=(Ο€^2 /6)ln2+∫_0 ^1 ((ln(1+x)ln(1βˆ’x))/x)dx ∫_0 ^1 ((ln(1+x)ln(1βˆ’x))/x)dx =(1/2)∫_0 ^1 ((ln^2 (1βˆ’x^2 )βˆ’ln^2 (1+x)βˆ’ln^2 (1βˆ’x))/x)dx =(1/2)∫_0 ^1 ((ln^2 (1βˆ’x^2 ))/x)dxβˆ’(1/2)∫_0 ^1 ((ln^2 (1+x))/x)βˆ’(1/2)∫_0 ^1 ((ln^2 (1βˆ’x))/x)dx =βˆ’βˆ«_0 ^1 ((ln(1βˆ’x^2 )lnx)/(1βˆ’x^2 ))(βˆ’2x)dxβˆ’(1/2)βˆ™((ΞΆ(3))/4)+∫_0 ^1 ((ln(1βˆ’x)lnx)/(1βˆ’x))(βˆ’1)dx =2∫_0 ^1 ((ln(1βˆ’x^2 )lnx)/(1βˆ’x^2 ))xdxβˆ’((ΞΆ(3))/8)βˆ’βˆ«_0 ^1 ((ln(1βˆ’x)lnx)/(1βˆ’x))dx =(1/2)∫_0 ^1 ((ln(1βˆ’u)lnu)/(1βˆ’u))duβˆ’((ΞΆ(3))/8)βˆ’βˆ«_0 ^1 ((ln(1βˆ’x)lnx)/(1βˆ’x))dx =βˆ’(1/2)∫_0 ^1 ((ln(1βˆ’x)lnx)/x)dxβˆ’((ΞΆ(3))/8) =βˆ’(1/2)∫_0 ^1 ((Li_2 (x))/x)dxβˆ’((ΞΆ(3))/8) =βˆ’(1/2)ΞΆ(3)βˆ’((ΞΆ(3))/8) =βˆ’(5/8)ΞΆ(3) β‡’Ο†=(Ο€^2 /6)ln2βˆ’(5/8)ΞΆ(3) βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’ ∫_0 ^1 ((ln(1βˆ’x)ln(1+x))/x)dx =Ξ£_(n=1) ^∞ (((βˆ’1)^(nβˆ’1) )/n)∫_0 ^1 x^(nβˆ’1) ln(1βˆ’x)dx =Ξ£_(n=1) ^∞ (((βˆ’1)^(nβˆ’1) )/n)(βˆ’(H_n /n)) =βˆ’Ξ£_(n=1) ^∞ (((βˆ’1)^(nβˆ’1) H_n )/n^2 ) =βˆ’(5/8)ΞΆ(3)
$$\phi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}βˆ’\mathrm{x}\right)}{\mathrm{2}βˆ’\mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\mathrm{ln2}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} \right)βˆ’\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)βˆ’\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}βˆ’\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}βˆ’\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=βˆ’\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}}{\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} }\left(βˆ’\mathrm{2x}\right)\mathrm{dx}βˆ’\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{lnx}}{\mathrm{1}βˆ’\mathrm{x}}\left(βˆ’\mathrm{1}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}}{\mathrm{1}βˆ’\mathrm{x}^{\mathrm{2}} }\mathrm{xdx}βˆ’\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}}βˆ’\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{lnx}}{\mathrm{1}βˆ’\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{u}\right)\mathrm{lnu}}{\mathrm{1}βˆ’\mathrm{u}}\mathrm{du}βˆ’\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}}βˆ’\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{lnx}}{\mathrm{1}βˆ’\mathrm{x}}\mathrm{dx} \\ $$$$=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}βˆ’\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}βˆ’\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$=βˆ’\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{3}\right)βˆ’\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$=βˆ’\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$\Rightarrow\phi=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\mathrm{ln2}βˆ’\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’βˆ’ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(βˆ’\mathrm{1}\right)^{\mathrm{n}βˆ’\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}βˆ’\mathrm{1}} \mathrm{ln}\left(\mathrm{1}βˆ’\mathrm{x}\right)\mathrm{dx} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(βˆ’\mathrm{1}\right)^{\mathrm{n}βˆ’\mathrm{1}} }{\mathrm{n}}\left(βˆ’\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}}\right) \\ $$$$=βˆ’\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(βˆ’\mathrm{1}\right)^{\mathrm{n}βˆ’\mathrm{1}} \mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=βˆ’\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$
Commented by mnjuly1970 last updated on 05/Jun/21
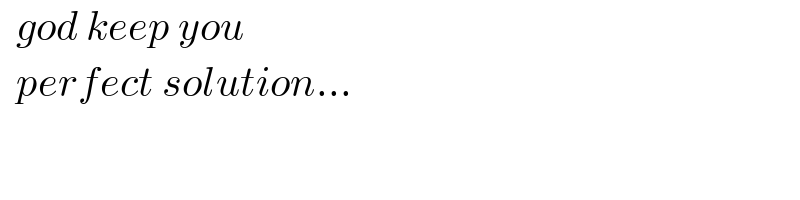
god keep you perfect solution...
$$\:\:{god}\:{keep}\:{you} \\ $$$$\:\:{perfect}\:{solution}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *