Menu Close

number-theory-Solve-in-Z-1-x-1-y-1-xy-1-4-

Tinku Tara 0 Comments
Pin




Question Number 142514 by mnjuly1970 last updated on 01/Jun/21
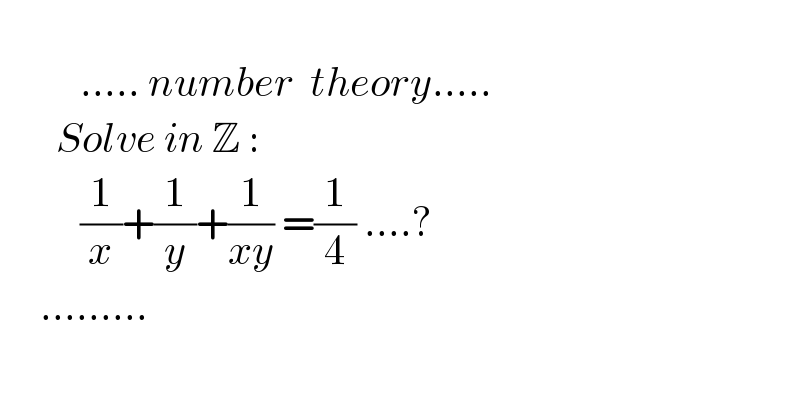
..... number theory..... Solve in Z : (1/x)+(1/y)+(1/(xy)) =(1/4) ....? .........
$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:…..\:{number}\:\:{theory}….. \\ $$$$\:\:\:\:\:\:\:{Solve}\:{in}\:\mathbb{Z}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{xy}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:….? \\ $$$$\:\:\:\:\:……… \\ $$
Answered by ArielVyny last updated on 01/Jun/21
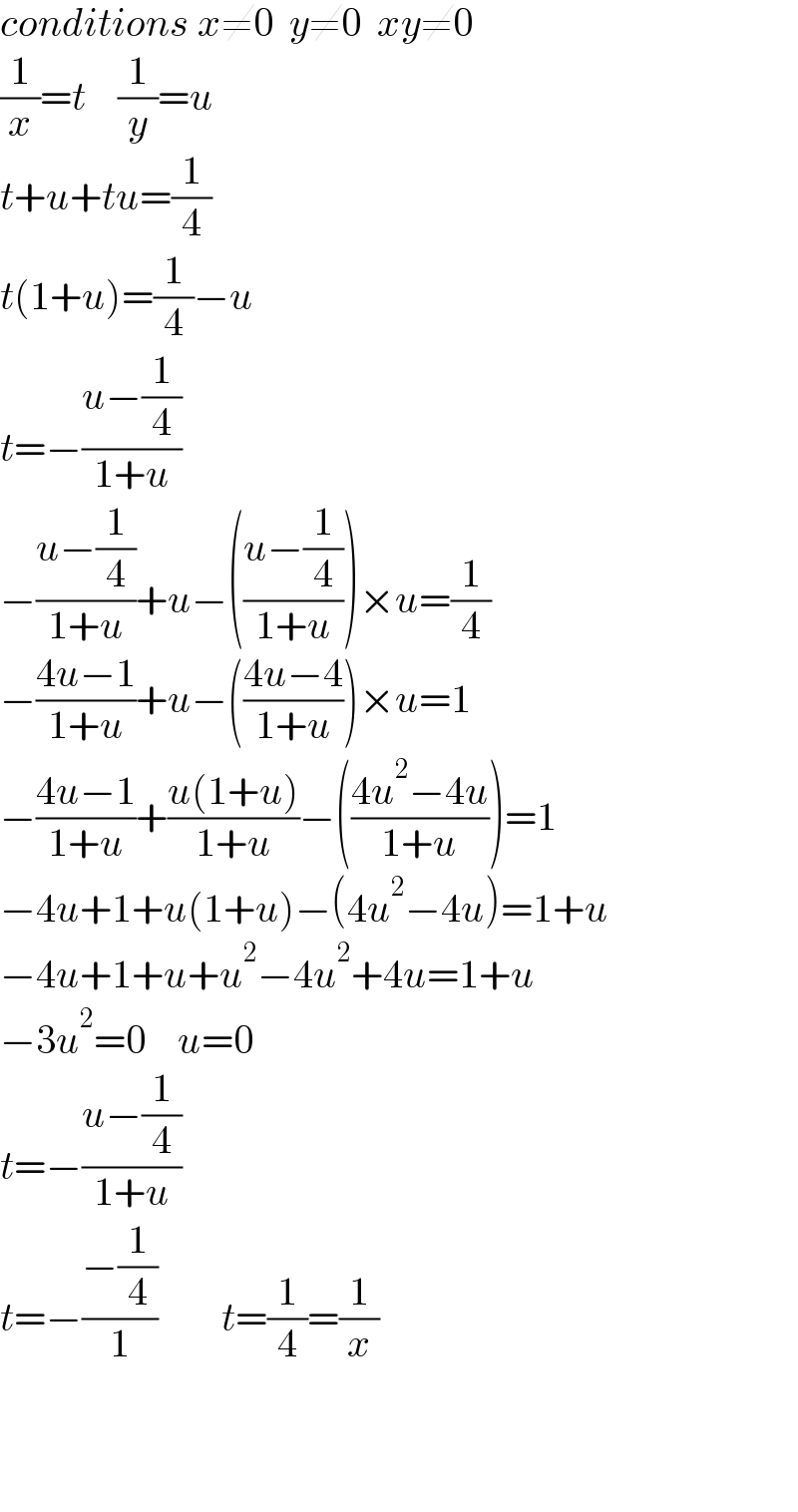
conditions x≠0 y≠0 xy≠0 (1/x)=t (1/y)=u t+u+tu=(1/4) t(1+u)=(1/4)−u t=−((u−(1/4))/(1+u)) −((u−(1/4))/(1+u))+u−(((u−(1/4))/(1+u)))×u=(1/4) −((4u−1)/(1+u))+u−(((4u−4)/(1+u)))×u=1 −((4u−1)/(1+u))+((u(1+u))/(1+u))−(((4u^2 −4u)/(1+u)))=1 −4u+1+u(1+u)−(4u^2 −4u)=1+u −4u+1+u+u^2 −4u^2 +4u=1+u −3u^2 =0 u=0 t=−((u−(1/4))/(1+u)) t=−((−(1/4))/1) t=(1/4)=(1/x)
$${conditions}\:{x}\neq\mathrm{0}\:\:{y}\neq\mathrm{0}\:\:{xy}\neq\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{x}}={t}\:\:\:\:\frac{\mathrm{1}}{{y}}={u} \\ $$$${t}+{u}+{tu}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${t}\left(\mathrm{1}+{u}\right)=\frac{\mathrm{1}}{\mathrm{4}}−{u} \\ $$$${t}=−\frac{{u}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}+{u}} \\ $$$$−\frac{{u}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}+{u}}+{u}−\left(\frac{{u}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}+{u}}\right)×{u}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$−\frac{\mathrm{4}{u}−\mathrm{1}}{\mathrm{1}+{u}}+{u}−\left(\frac{\mathrm{4}{u}−\mathrm{4}}{\mathrm{1}+{u}}\right)×{u}=\mathrm{1} \\ $$$$−\frac{\mathrm{4}{u}−\mathrm{1}}{\mathrm{1}+{u}}+\frac{{u}\left(\mathrm{1}+{u}\right)}{\mathrm{1}+{u}}−\left(\frac{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{u}}{\mathrm{1}+{u}}\right)=\mathrm{1} \\ $$$$−\mathrm{4}{u}+\mathrm{1}+{u}\left(\mathrm{1}+{u}\right)−\left(\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}{u}\right)=\mathrm{1}+{u} \\ $$$$−\mathrm{4}{u}+\mathrm{1}+{u}+{u}^{\mathrm{2}} −\mathrm{4}{u}^{\mathrm{2}} +\mathrm{4}{u}=\mathrm{1}+{u} \\ $$$$−\mathrm{3}{u}^{\mathrm{2}} =\mathrm{0}\:\:\:\:{u}=\mathrm{0} \\ $$$${t}=−\frac{{u}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}+{u}} \\ $$$${t}=−\frac{−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}}\:\:\:\:\:\:\:\:{t}=\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{{x}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by ArielVyny last updated on 01/Jun/21
it is possible ?
$${it}\:{is}\:{possible}\:? \\ $$
Answered by ArielVyny last updated on 01/Jun/21
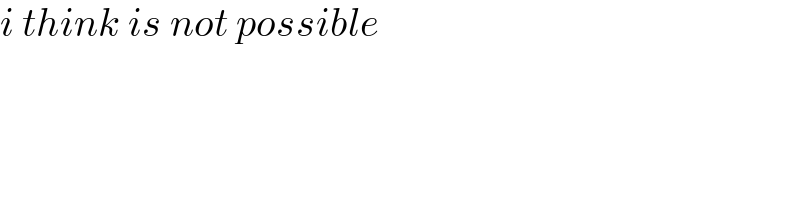
i think is not possible
$${i}\:{think}\:{is}\:{not}\:{possible} \\ $$
Answered by ajfour last updated on 01/Jun/21
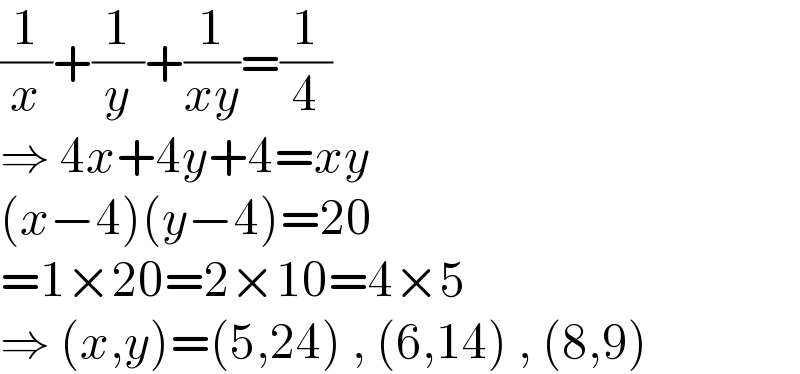
(1/x)+(1/y)+(1/(xy))=(1/4) ⇒ 4x+4y+4=xy (x−4)(y−4)=20 =1×20=2×10=4×5 ⇒ (x,y)=(5,24) , (6,14) , (8,9)
$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{xy}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{4}{x}+\mathrm{4}{y}+\mathrm{4}={xy} \\ $$$$\left({x}−\mathrm{4}\right)\left({y}−\mathrm{4}\right)=\mathrm{20} \\ $$$$=\mathrm{1}×\mathrm{20}=\mathrm{2}×\mathrm{10}=\mathrm{4}×\mathrm{5} \\ $$$$\Rightarrow\:\left({x},{y}\right)=\left(\mathrm{5},\mathrm{24}\right)\:,\:\left(\mathrm{6},\mathrm{14}\right)\:,\:\left(\mathrm{8},\mathrm{9}\right) \\ $$
Commented by mnjuly1970 last updated on 01/Jun/21
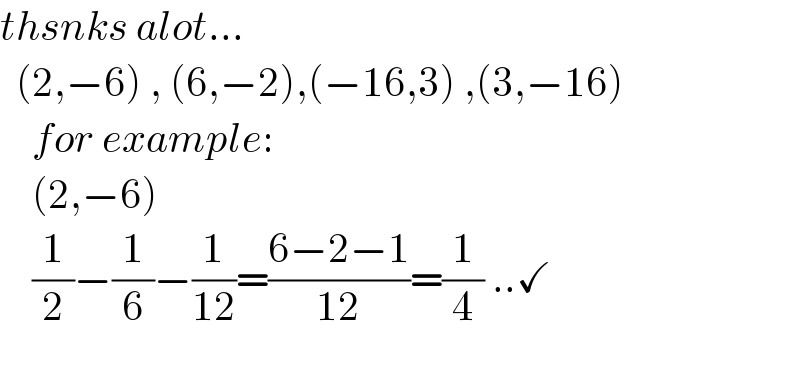
thsnks alot... (2,−6) , (6,−2),(−16,3) ,(3,−16) for example: (2,−6) (1/2)−(1/6)−(1/(12))=((6−2−1)/(12))=(1/4) ..✓
$${thsnks}\:{alot}… \\ $$$$\:\:\left(\mathrm{2},−\mathrm{6}\right)\:,\:\left(\mathrm{6},−\mathrm{2}\right),\left(−\mathrm{16},\mathrm{3}\right)\:,\left(\mathrm{3},−\mathrm{16}\right) \\ $$$$\:\:\:\:{for}\:{example}: \\ $$$$\:\:\:\:\left(\mathrm{2},−\mathrm{6}\right) \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{6}−\mathrm{2}−\mathrm{1}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{4}}\:..\checkmark \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 01/Jun/21
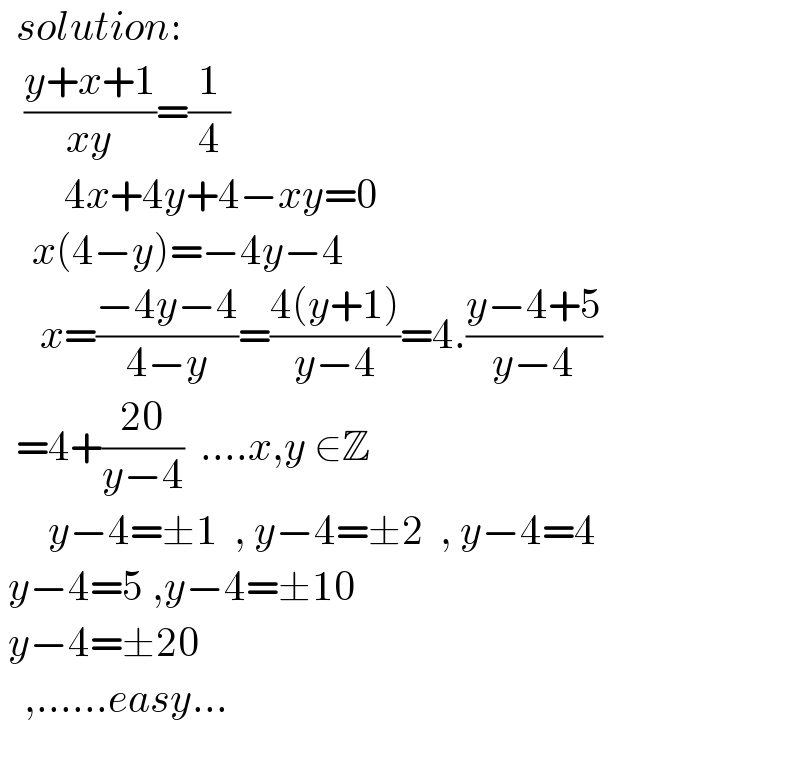
solution: ((y+x+1)/(xy))=(1/4) 4x+4y+4−xy=0 x(4−y)=−4y−4 x=((−4y−4)/(4−y))=((4(y+1))/(y−4))=4.((y−4+5)/(y−4)) =4+((20)/(y−4)) ....x,y ∈Z y−4=±1 , y−4=±2 , y−4=4 y−4=5 ,y−4=±10 y−4=±20 ,......easy...
$$\:\:{solution}: \\ $$$$\:\:\:\frac{{y}+{x}+\mathrm{1}}{{xy}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}{x}+\mathrm{4}{y}+\mathrm{4}−{xy}=\mathrm{0} \\ $$$$\:\:\:\:{x}\left(\mathrm{4}−{y}\right)=−\mathrm{4}{y}−\mathrm{4} \\ $$$$\:\:\:\:\:{x}=\frac{−\mathrm{4}{y}−\mathrm{4}}{\mathrm{4}−{y}}=\frac{\mathrm{4}\left({y}+\mathrm{1}\right)}{{y}−\mathrm{4}}=\mathrm{4}.\frac{{y}−\mathrm{4}+\mathrm{5}}{{y}−\mathrm{4}} \\ $$$$\:\:=\mathrm{4}+\frac{\mathrm{20}}{{y}−\mathrm{4}}\:\:….{x},{y}\:\in\mathbb{Z} \\ $$$$\:\:\:\:\:\:{y}−\mathrm{4}=\pm\mathrm{1}\:\:,\:{y}−\mathrm{4}=\pm\mathrm{2}\:\:,\:{y}−\mathrm{4}=\mathrm{4} \\ $$$$\:{y}−\mathrm{4}=\mathrm{5}\:,{y}−\mathrm{4}=\pm\mathrm{10} \\ $$$$\:{y}−\mathrm{4}=\pm\mathrm{20} \\ $$$$\:\:\:,……{easy}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *