Question Number 131805 by Engr_Jidda last updated on 08/Feb/21
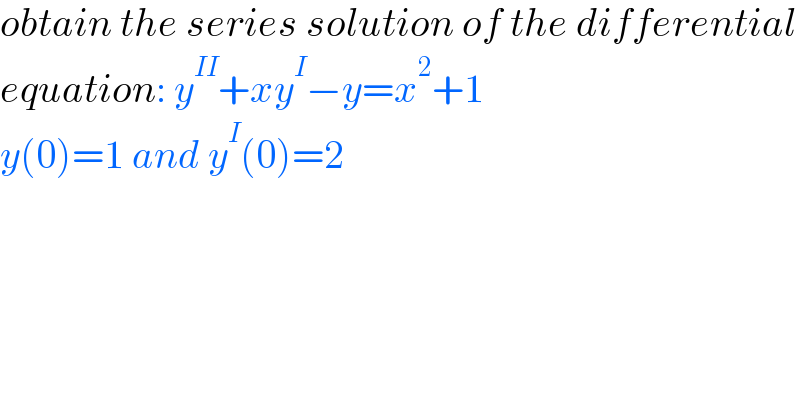
$${obtain}\:{the}\:{series}\:{solution}\:{of}\:{the}\:{differential}\: \\ $$$${equation}:\:{y}^{{II}} +{xy}^{{I}} −{y}={x}^{\mathrm{2}} +\mathrm{1} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{1}\:{and}\:{y}^{{I}} \left(\mathrm{0}\right)=\mathrm{2} \\ $$
Answered by physicstutes last updated on 08/Feb/21
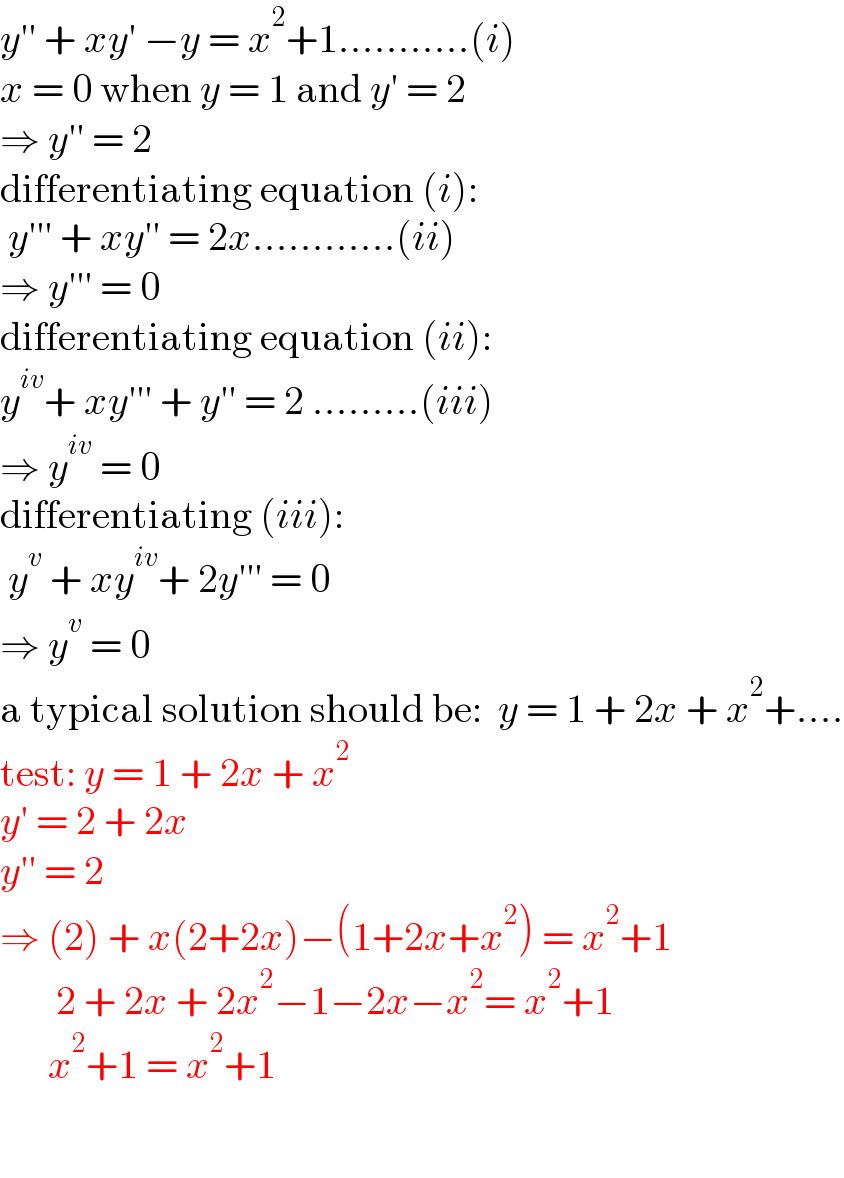
$${y}''\:+\:{xy}'\:−{y}\:=\:{x}^{\mathrm{2}} +\mathrm{1}………..\left({i}\right) \\ $$$${x}\:=\:\mathrm{0}\:\mathrm{when}\:{y}\:=\:\mathrm{1}\:\mathrm{and}\:{y}'\:=\:\mathrm{2} \\ $$$$\Rightarrow\:{y}''\:=\:\mathrm{2} \\ $$$$\mathrm{differentiating}\:\mathrm{equation}\:\left({i}\right): \\ $$$$\:{y}'''\:+\:{xy}''\:=\:\mathrm{2}{x}…………\left({ii}\right) \\ $$$$\Rightarrow\:{y}'''\:=\:\mathrm{0} \\ $$$$\mathrm{differentiating}\:\mathrm{equation}\:\left({ii}\right): \\ $$$${y}^{{iv}} +\:{xy}'''\:+\:{y}''\:=\:\mathrm{2}\:………\left({iii}\right) \\ $$$$\Rightarrow\:{y}^{{iv}} \:=\:\mathrm{0} \\ $$$$\mathrm{differentiating}\:\left({iii}\right): \\ $$$$\:{y}^{{v}} \:+\:{xy}^{{iv}} +\:\mathrm{2}{y}'''\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{y}^{{v}} \:=\:\mathrm{0} \\ $$$$\mathrm{a}\:\mathrm{typical}\:\mathrm{solution}\:\mathrm{should}\:\mathrm{be}:\:\:{y}\:=\:\mathrm{1}\:+\:\mathrm{2}{x}\:+\:{x}^{\mathrm{2}} +…. \\ $$$$\mathrm{test}:\:{y}\:=\:\mathrm{1}\:+\:\mathrm{2}{x}\:+\:{x}^{\mathrm{2}} \\ $$$${y}'\:=\:\mathrm{2}\:+\:\mathrm{2}{x} \\ $$$${y}''\:=\:\mathrm{2} \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)\:+\:{x}\left(\mathrm{2}+\mathrm{2}{x}\right)−\left(\mathrm{1}+\mathrm{2}{x}+{x}^{\mathrm{2}} \right)\:=\:{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}\:+\:\mathrm{2}{x}\:+\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{2}{x}−{x}^{\mathrm{2}} =\:{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{1}\:=\:{x}^{\mathrm{2}} +\mathrm{1}\: \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Commented by Engr_Jidda last updated on 08/Feb/21

$${thank}\:{you}\:{sir} \\ $$
