p-is-a-prime-number-such-that-1-p-p-2-7-find-all-k-such-that-p-k-42-

Question Number 67481 by Mohamed Amine Bouguezzoul last updated on 27/Aug/19

p i s a p r i m e n u m b e r s u c h t h a t {(1 + p)}^{p} \equiv 2 [7]

f i n d a l l k s u c h t h a t p \equiv k [42]

Commented by Rasheed.Sindhi last updated on 30/Aug/19

S o m e v a l u e s o f k

{(1 + 2)}^{2} \equiv 2 [7] \Rightarrow 2 \equiv 2 [42] \Rightarrow k = 2

{(1 + 17)}^{17} \equiv 2 [7] \Rightarrow 17 \equiv 17 [42] \Rightarrow k = 17

{(1 + 43)}^{43} \equiv 2 [7] \Rightarrow 43 \equiv 1 [42] \Rightarrow k = 1

\dots . .

Commented by Mohamed Amine Bouguezzoul last updated on 30/Aug/19

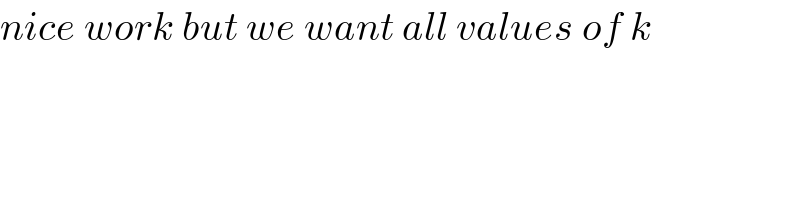
n i c e w o r k b u t w e w a n t a l l v a l u e s o f k