Question Number 7651 by FilupSmith last updated on 07/Sep/16

$${P}=\underset{{n}=\mathrm{1}} {\overset{{k}} {\prod}}{n}^{{n}} \\ $$$${P}=??? \\ $$
Commented by FilupSmith last updated on 07/Sep/16
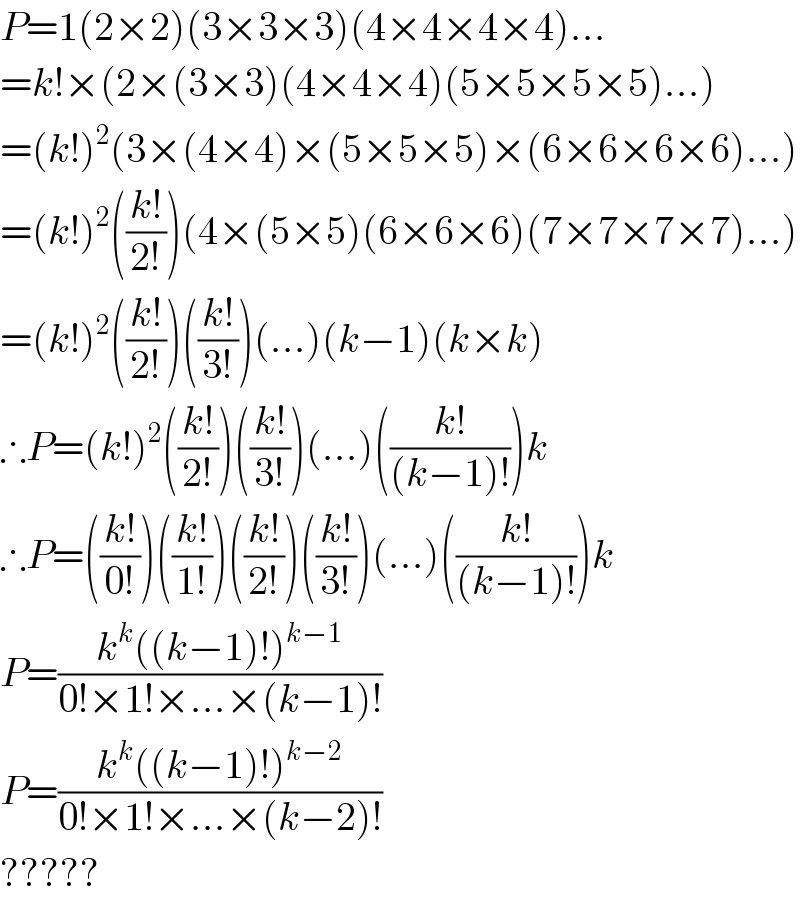
$${P}=\mathrm{1}\left(\mathrm{2}×\mathrm{2}\right)\left(\mathrm{3}×\mathrm{3}×\mathrm{3}\right)\left(\mathrm{4}×\mathrm{4}×\mathrm{4}×\mathrm{4}\right)… \\ $$$$={k}!×\left(\mathrm{2}×\left(\mathrm{3}×\mathrm{3}\right)\left(\mathrm{4}×\mathrm{4}×\mathrm{4}\right)\left(\mathrm{5}×\mathrm{5}×\mathrm{5}×\mathrm{5}\right)…\right) \\ $$$$=\left({k}!\right)^{\mathrm{2}} \left(\mathrm{3}×\left(\mathrm{4}×\mathrm{4}\right)×\left(\mathrm{5}×\mathrm{5}×\mathrm{5}\right)×\left(\mathrm{6}×\mathrm{6}×\mathrm{6}×\mathrm{6}\right)…\right) \\ $$$$=\left({k}!\right)^{\mathrm{2}} \left(\frac{{k}!}{\mathrm{2}!}\right)\left(\mathrm{4}×\left(\mathrm{5}×\mathrm{5}\right)\left(\mathrm{6}×\mathrm{6}×\mathrm{6}\right)\left(\mathrm{7}×\mathrm{7}×\mathrm{7}×\mathrm{7}\right)…\right) \\ $$$$=\left({k}!\right)^{\mathrm{2}} \left(\frac{{k}!}{\mathrm{2}!}\right)\left(\frac{{k}!}{\mathrm{3}!}\right)\left(…\right)\left({k}−\mathrm{1}\right)\left({k}×{k}\right) \\ $$$$\therefore{P}=\left({k}!\right)^{\mathrm{2}} \left(\frac{{k}!}{\mathrm{2}!}\right)\left(\frac{{k}!}{\mathrm{3}!}\right)\left(…\right)\left(\frac{{k}!}{\left({k}−\mathrm{1}\right)!}\right){k} \\ $$$$\therefore{P}=\left(\frac{{k}!}{\mathrm{0}!}\right)\left(\frac{{k}!}{\mathrm{1}!}\right)\left(\frac{{k}!}{\mathrm{2}!}\right)\left(\frac{{k}!}{\mathrm{3}!}\right)\left(…\right)\left(\frac{{k}!}{\left({k}−\mathrm{1}\right)!}\right){k} \\ $$$${P}=\frac{{k}^{{k}} \left(\left({k}−\mathrm{1}\right)!\right)^{{k}−\mathrm{1}} }{\mathrm{0}!×\mathrm{1}!×…×\left({k}−\mathrm{1}\right)!} \\ $$$${P}=\frac{{k}^{{k}} \left(\left({k}−\mathrm{1}\right)!\right)^{{k}−\mathrm{2}} }{\mathrm{0}!×\mathrm{1}!×…×\left({k}−\mathrm{2}\right)!} \\ $$$$????? \\ $$
Commented by 123456 last updated on 08/Sep/16

$${P}=\left(\frac{{k}!}{\mathrm{0}!}\right)\left(\frac{{k}!}{\mathrm{1}!}\right)…\left(\frac{{k}!}{\left({k}−\mathrm{1}\right)!}\right){k}=\frac{\left({k}!\right)^{{k}} {k}}{\mathrm{0}!×\mathrm{1}!×\centerdot\centerdot\centerdot×\left({k}−\mathrm{1}\right)!} \\ $$$${P}=\frac{\left({k}\left({k}−\mathrm{1}\right)!\right)^{{k}} {k}}{\mathrm{0}!×\mathrm{1}!×\centerdot\centerdot\centerdot×\left({k}−\mathrm{1}\right)!} \\ $$$${P}=\frac{{k}^{{k}+\mathrm{1}} \left(\left({k}−\mathrm{1}\right)!\right)^{{k}−\mathrm{1}} }{\mathrm{0}!×\mathrm{1}!×….×\left({k}−\mathrm{2}\right)!} \\ $$
