Question Number 7723 by FilupSmith last updated on 12/Sep/16
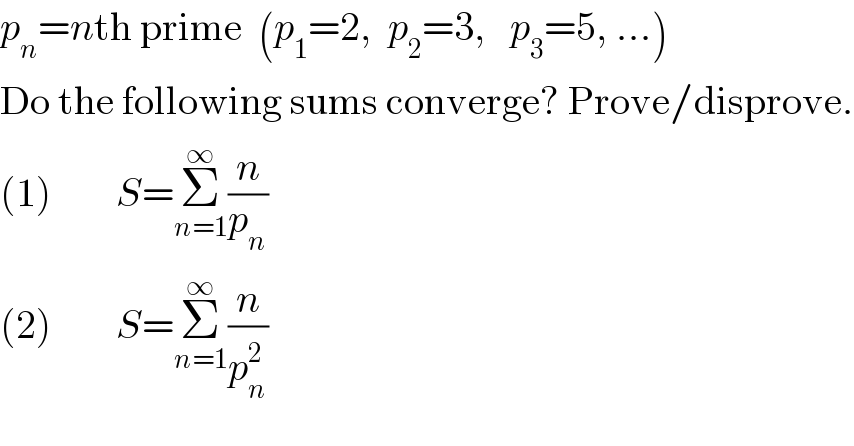
$${p}_{{n}} ={n}\mathrm{th}\:\mathrm{prime}\:\:\left({p}_{\mathrm{1}} =\mathrm{2},\:\:{p}_{\mathrm{2}} =\mathrm{3},\:\:\:{p}_{\mathrm{3}} =\mathrm{5},\:…\right) \\ $$$$\mathrm{Do}\:\mathrm{the}\:\mathrm{following}\:\mathrm{sums}\:\mathrm{converge}?\:\mathrm{Prove}/\mathrm{disprove}. \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:{S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{p}_{{n}} } \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:{S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{p}_{{n}} ^{\mathrm{2}} } \\ $$
Commented by FilupSmith last updated on 12/Sep/16
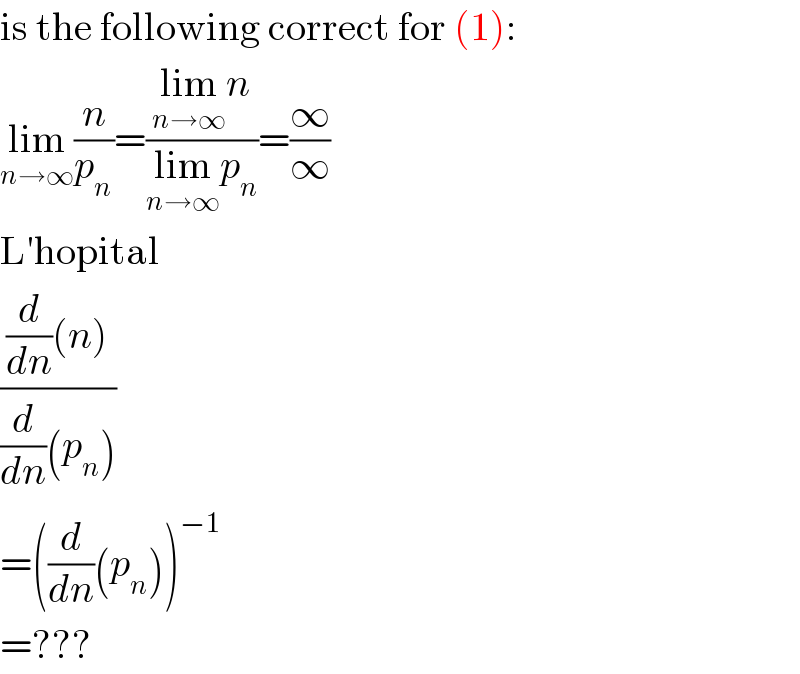
$$\mathrm{is}\:\mathrm{the}\:\mathrm{following}\:\mathrm{correct}\:\mathrm{for}\:\left(\mathrm{1}\right): \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{{p}_{{n}} }=\frac{\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}}{\underset{{n}\rightarrow\infty} {\mathrm{lim}}{p}_{{n}} }=\frac{\infty}{\infty} \\ $$$$\mathrm{L}'\mathrm{hopital} \\ $$$$\frac{\frac{{d}}{{dn}}\left({n}\right)}{\frac{{d}}{{dn}}\left({p}_{{n}} \right)} \\ $$$$=\left(\frac{{d}}{{dn}}\left({p}_{{n}} \right)\right)^{−\mathrm{1}} \\ $$$$=??? \\ $$
