Question Number 133036 by liberty last updated on 18/Feb/21
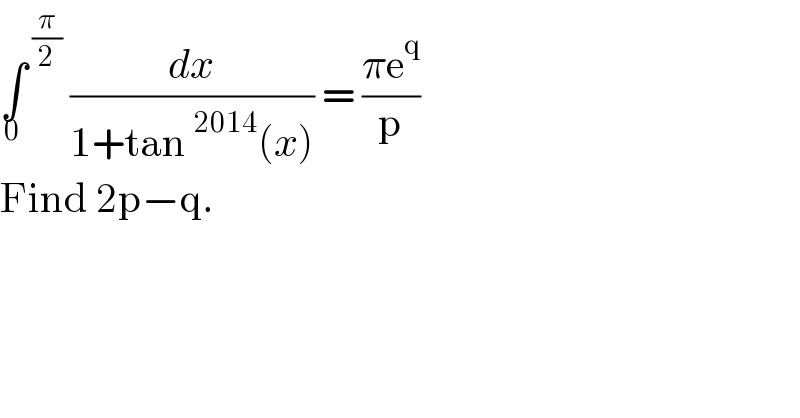
$$\underset{\mathrm{0}} {\int}^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left({x}\right)}\:=\:\frac{\pi\mathrm{e}^{\mathrm{q}} }{\mathrm{p}} \\ $$$$\mathrm{Find}\:\mathrm{2p}−\mathrm{q}.\: \\ $$
Answered by liberty last updated on 18/Feb/21
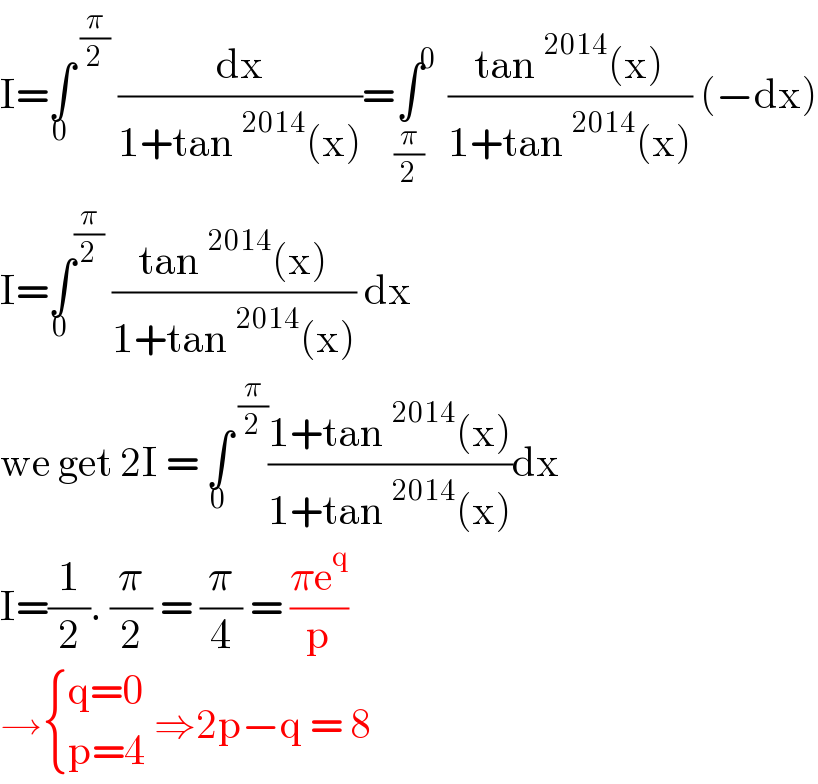
$$\mathrm{I}=\underset{\mathrm{0}} {\int}^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}=\underset{\frac{\pi}{\mathrm{2}}} {\int}^{\mathrm{0}} \:\frac{\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}\:\left(−\mathrm{dx}\right) \\ $$$$\mathrm{I}=\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}\:\mathrm{dx}\: \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{2I}\:=\:\underset{\mathrm{0}} {\int}^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2014}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}.\:\frac{\pi}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{4}}\:=\:\frac{\pi\mathrm{e}^{\mathrm{q}} }{\mathrm{p}} \\ $$$$\rightarrow\begin{cases}{\mathrm{q}=\mathrm{0}}\\{\mathrm{p}=\mathrm{4}}\end{cases}\:\Rightarrow\mathrm{2p}−\mathrm{q}\:=\:\mathrm{8}\: \\ $$
Answered by mathmax by abdo last updated on 20/Feb/21
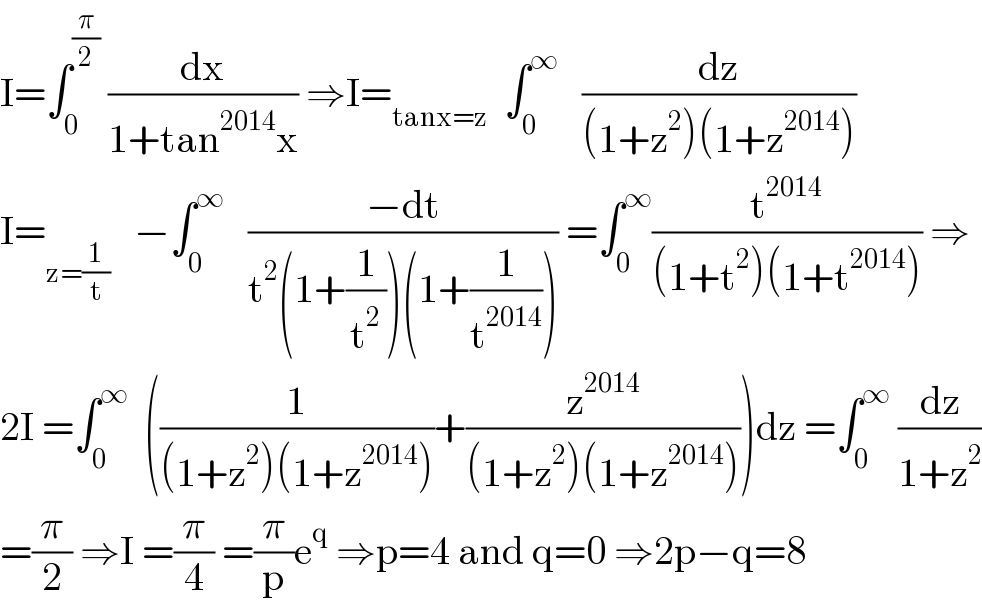
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2014}} \mathrm{x}}\:\Rightarrow\mathrm{I}=_{\mathrm{tanx}=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dz}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2014}} \right)} \\ $$$$\mathrm{I}=_{\mathrm{z}=\frac{\mathrm{1}}{\mathrm{t}}} \:\:\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{−\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2014}} }\right)}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2014}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2014}} \right)}\:\Rightarrow \\ $$$$\mathrm{2I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2014}} \right)}+\frac{\mathrm{z}^{\mathrm{2014}} }{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2014}} \right)}\right)\mathrm{dz}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{I}\:=\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{p}}\mathrm{e}^{\mathrm{q}} \:\Rightarrow\mathrm{p}=\mathrm{4}\:\mathrm{and}\:\mathrm{q}=\mathrm{0}\:\Rightarrow\mathrm{2p}−\mathrm{q}=\mathrm{8} \\ $$
