Question Number 132901 by bramlexs22 last updated on 17/Feb/21

$$\int_{−\pi/\mathrm{2}} ^{\mathrm{3}\pi/\mathrm{2}} \:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mid\mathrm{sin}\:\mathrm{x}\mid\right)+\mathrm{cos}^{−\mathrm{1}} \left(\mid\mathrm{cos}\:\mathrm{x}\mid\right)\right)\:\mathrm{dx} \\ $$
Answered by liberty last updated on 17/Feb/21
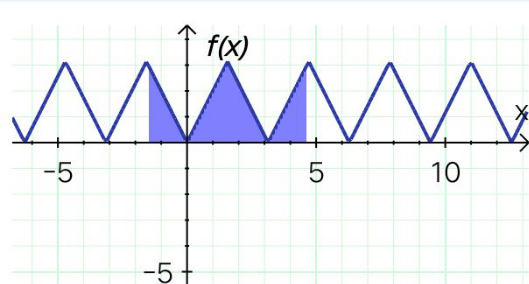
Commented by liberty last updated on 17/Feb/21

$$ \\ $$$$=\:\pi^{\mathrm{2}} \:\approx\:\mathrm{9}.\mathrm{8696044} \\ $$
Answered by Ñï= last updated on 17/Feb/21
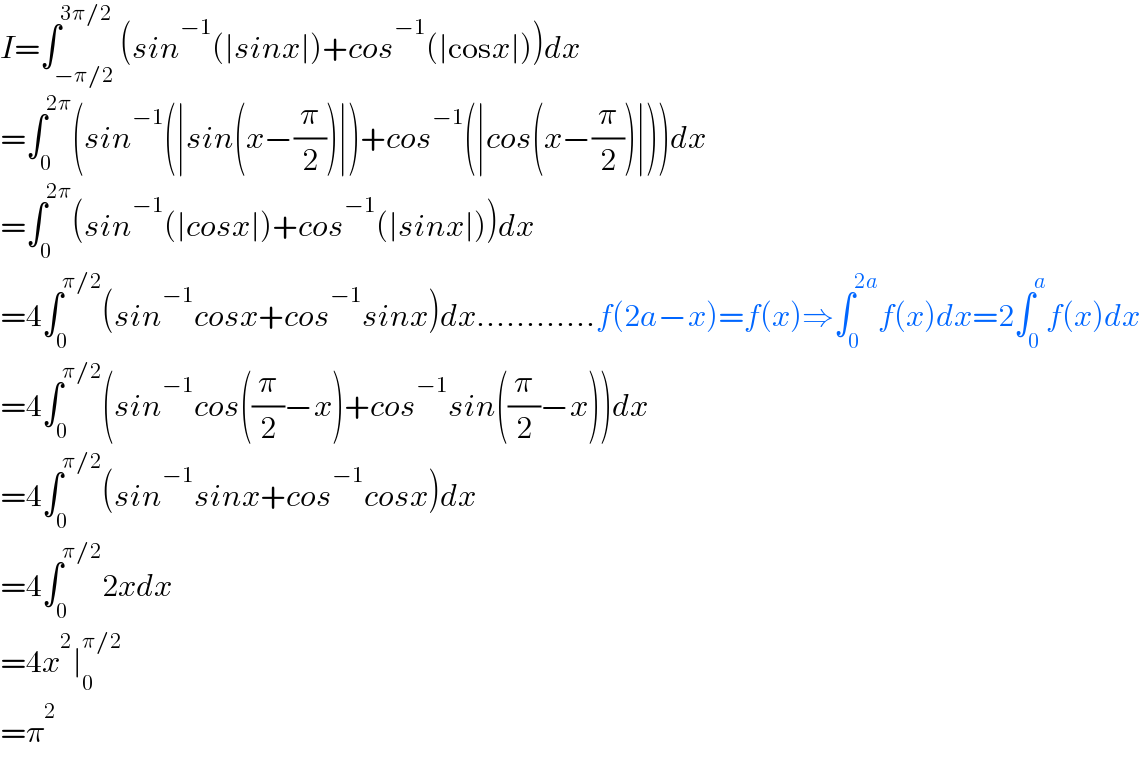
$${I}=\int_{−\pi/\mathrm{2}} ^{\mathrm{3}\pi/\mathrm{2}} \left({sin}^{−\mathrm{1}} \left(\mid{sinx}\mid\right)+{cos}^{−\mathrm{1}} \left(\mid\mathrm{cos}{x}\mid\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({sin}^{−\mathrm{1}} \left(\mid{sin}\left({x}−\frac{\pi}{\mathrm{2}}\right)\mid\right)+{cos}^{−\mathrm{1}} \left(\mid{cos}\left({x}−\frac{\pi}{\mathrm{2}}\right)\mid\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({sin}^{−\mathrm{1}} \left(\mid{cosx}\mid\right)+{cos}^{−\mathrm{1}} \left(\mid{sinx}\mid\right)\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({sin}^{−\mathrm{1}} {cosx}+{cos}^{−\mathrm{1}} {sinx}\right){dx}…………{f}\left(\mathrm{2}{a}−{x}\right)={f}\left({x}\right)\Rightarrow\int_{\mathrm{0}} ^{\mathrm{2}{a}} {f}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({sin}^{−\mathrm{1}} {cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+{cos}^{−\mathrm{1}} {sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({sin}^{−\mathrm{1}} {sinx}+{cos}^{−\mathrm{1}} {cosx}\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{2}{xdx} \\ $$$$=\mathrm{4}{x}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\pi^{\mathrm{2}} \\ $$
