Question Number 630 by 123456 last updated on 15/Feb/15

$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{+\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}{dx} \\ $$$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{+\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\mathrm{cos}\left(\mathrm{2}{nx}\right){dx} \\ $$$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{+\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\mathrm{sin}\left(\mathrm{2}{nx}\right){dx} \\ $$$${n}\in\mathbb{N}^{\ast} \\ $$
Commented by prakash jain last updated on 15/Feb/15
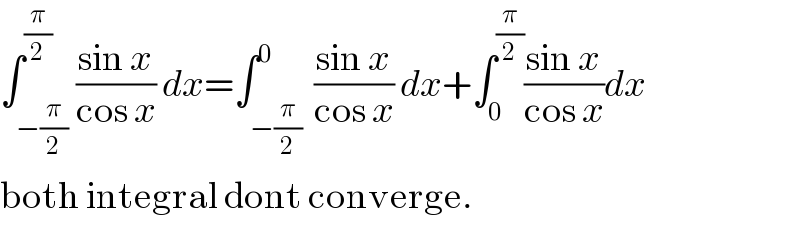
$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\:{dx}=\int_{−\frac{\pi}{\mathrm{2}}\:} ^{\mathrm{0}} \frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\:{dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}{dx} \\ $$$$\mathrm{both}\:\mathrm{integral}\:\mathrm{dont}\:\mathrm{converge}. \\ $$
