Question Number 141269 by ajfour last updated on 17/May/21
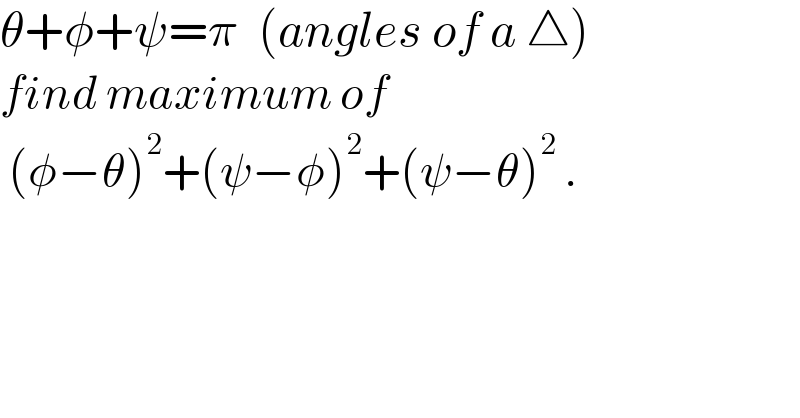
$$\theta+\phi+\psi=\pi\:\:\left({angles}\:{of}\:{a}\:\bigtriangleup\right) \\ $$$${find}\:{maximum}\:{of} \\ $$$$\:\left(\phi−\theta\right)^{\mathrm{2}} +\left(\psi−\phi\right)^{\mathrm{2}} +\left(\psi−\theta\right)^{\mathrm{2}} \:. \\ $$
Commented by MJS_new last updated on 17/May/21
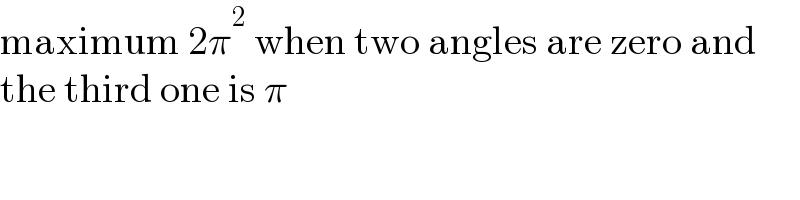
$$\mathrm{maximum}\:\mathrm{2}\pi^{\mathrm{2}} \:\mathrm{when}\:\mathrm{two}\:\mathrm{angles}\:\mathrm{are}\:\mathrm{zero}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{third}\:\mathrm{one}\:\mathrm{is}\:\pi \\ $$
Commented by ajfour last updated on 17/May/21
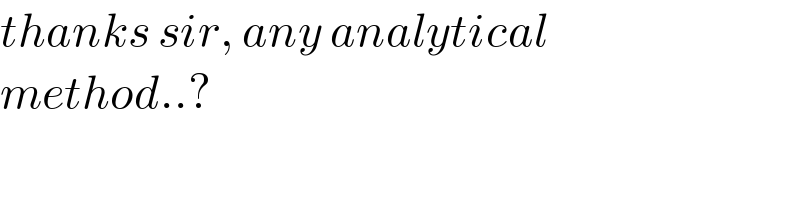
$${thanks}\:{sir},\:{any}\:{analytical} \\ $$$${method}..? \\ $$
Commented by MJS_new last updated on 17/May/21
![sorry for using a, b, c instead of your variable names, I′m in a hurry (1) c=π−a−b ⇒ 6a^2 +6ab+6b^2 −6πa−6πb+2π^2 → max (d/db)[...]=6a+12b−6π=0 ⇒ b=((π−a)/2) but this leads to a=b=c=(π/3) and a minimum ⇒ we have to search along the borders 0≤a, b≤π b=0 6a^2 −6πa+2π^2 → max again only a minimum ⇒ a=0∨a=π ⇒ max = 2π^2](https://www.tinkutara.com/question/Q141316.png)
$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{using}\:{a},\:{b},\:{c}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{your}\:\mathrm{variable} \\ $$$$\mathrm{names},\:\mathrm{I}'\mathrm{m}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry} \\ $$$$\left(\mathrm{1}\right) \\ $$$${c}=\pi−{a}−{b} \\ $$$$\Rightarrow \\ $$$$\mathrm{6}{a}^{\mathrm{2}} +\mathrm{6}{ab}+\mathrm{6}{b}^{\mathrm{2}} −\mathrm{6}\pi{a}−\mathrm{6}\pi{b}+\mathrm{2}\pi^{\mathrm{2}} \:\rightarrow\:\mathrm{max} \\ $$$$\frac{{d}}{{db}}\left[…\right]=\mathrm{6}{a}+\mathrm{12}{b}−\mathrm{6}\pi=\mathrm{0}\:\Rightarrow\:{b}=\frac{\pi−{a}}{\mathrm{2}} \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:{a}={b}={c}=\frac{\pi}{\mathrm{3}}\:\mathrm{and}\:\mathrm{a}\:\mathrm{minimum} \\ $$$$\Rightarrow \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{search}\:\mathrm{along}\:\mathrm{the}\:\mathrm{borders} \\ $$$$\mathrm{0}\leqslant{a},\:{b}\leqslant\pi \\ $$$${b}=\mathrm{0} \\ $$$$\mathrm{6}{a}^{\mathrm{2}} −\mathrm{6}\pi{a}+\mathrm{2}\pi^{\mathrm{2}} \:\rightarrow\:\mathrm{max} \\ $$$$\mathrm{again}\:\mathrm{only}\:\mathrm{a}\:\mathrm{minimum}\:\Rightarrow \\ $$$${a}=\mathrm{0}\vee{a}=\pi\:\Rightarrow\:\mathrm{max}\:=\:\mathrm{2}\pi^{\mathrm{2}} \\ $$
Answered by TheSupreme last updated on 17/May/21
![Γ(∅,θ)=f(∅,θ,π−∅−θ)=(∅−θ)^2 +(π−2∅−θ)^2 +(π−∅−2θ)^2 grad Γ= { ((2(∅−θ)−4(π−2∅−θ)−2(π−∅−2θ)=0)),((−2(∅−θ)−2(π−2∅−θ)−4(π−∅−2θ)=0)) :} { ((2∅+θ=π)),((∅+2θ=π)) :} (∅,θ)=((π/3),(π/3)) Γ((π/3),(π/3))=0 (absolute min) set ∅=kθ Λ(θ,k)=f(kθ,θ,π−kθ−θ)=θ^2 (k−1)^2 +(π−2kθ−θ)^2 +(π−kθ−2θ)^2 θ^2 [(k−1)^2 +(2k+1)^2 +(k+2)^2 ]−2θπ[(2k+1)+(k+2)]+2π^2 as you can see f is not limited f has no max](https://www.tinkutara.com/question/Q141279.png)
$$\Gamma\left(\emptyset,\theta\right)={f}\left(\emptyset,\theta,\pi−\emptyset−\theta\right)=\left(\emptyset−\theta\right)^{\mathrm{2}} +\left(\pi−\mathrm{2}\emptyset−\theta\right)^{\mathrm{2}} +\left(\pi−\emptyset−\mathrm{2}\theta\right)^{\mathrm{2}} \\ $$$${grad}\:\Gamma=\begin{cases}{\mathrm{2}\left(\emptyset−\theta\right)−\mathrm{4}\left(\pi−\mathrm{2}\emptyset−\theta\right)−\mathrm{2}\left(\pi−\emptyset−\mathrm{2}\theta\right)=\mathrm{0}}\\{−\mathrm{2}\left(\emptyset−\theta\right)−\mathrm{2}\left(\pi−\mathrm{2}\emptyset−\theta\right)−\mathrm{4}\left(\pi−\emptyset−\mathrm{2}\theta\right)=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{\mathrm{2}\emptyset+\theta=\pi}\\{\emptyset+\mathrm{2}\theta=\pi}\end{cases} \\ $$$$\left(\emptyset,\theta\right)=\left(\frac{\pi}{\mathrm{3}},\frac{\pi}{\mathrm{3}}\right) \\ $$$$\Gamma\left(\frac{\pi}{\mathrm{3}},\frac{\pi}{\mathrm{3}}\right)=\mathrm{0}\:\left({absolute}\:{min}\right) \\ $$$$ \\ $$$${set}\:\emptyset={k}\theta \\ $$$$\Lambda\left(\theta,{k}\right)={f}\left({k}\theta,\theta,\pi−{k}\theta−\theta\right)=\theta^{\mathrm{2}} \left({k}−\mathrm{1}\right)^{\mathrm{2}} +\left(\pi−\mathrm{2}{k}\theta−\theta\right)^{\mathrm{2}} +\left(\pi−{k}\theta−\mathrm{2}\theta\right)^{\mathrm{2}} \\ $$$$\theta^{\mathrm{2}} \left[\left({k}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} +\left({k}+\mathrm{2}\right)^{\mathrm{2}} \right]−\mathrm{2}\theta\pi\left[\left(\mathrm{2}{k}+\mathrm{1}\right)+\left({k}+\mathrm{2}\right)\right]+\mathrm{2}\pi^{\mathrm{2}} \\ $$$${as}\:{you}\:{can}\:{see}\:{f}\:{is}\:{not}\:{limited} \\ $$$${f}\:{has}\:{no}\:{max} \\ $$
