Question Number 70310 by Rio Michael last updated on 03/Oct/19

$${please}\:{help}\:{me}\:{find}\:{the}\:{term}\:{independent}\:{of}\:{x} \\ $$$${in}\:{the}\:{expansion}\:{of}\: \\ $$$$\:\:\:\:\:\:\left({x}\:+\:\frac{\mathrm{3}}{{x}}\right)^{−\mathrm{12}\:} \\ $$
Commented by mr W last updated on 03/Oct/19

$${all}\:{terms}\:{are}\:{x}\:{dependent}! \\ $$
Answered by MJS last updated on 03/Oct/19
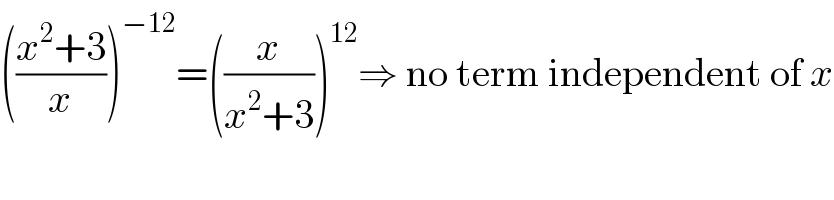
$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}}\right)^{−\mathrm{12}} =\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\mathrm{12}} \Rightarrow\:\mathrm{no}\:\mathrm{term}\:\mathrm{independent}\:\mathrm{of}\:{x} \\ $$
Answered by mind is power last updated on 03/Oct/19

$$\left({x}+\frac{\mathrm{3}}{{x}}\right)^{\mathrm{12}} ? \\ $$
Commented by Kunal12588 last updated on 03/Oct/19
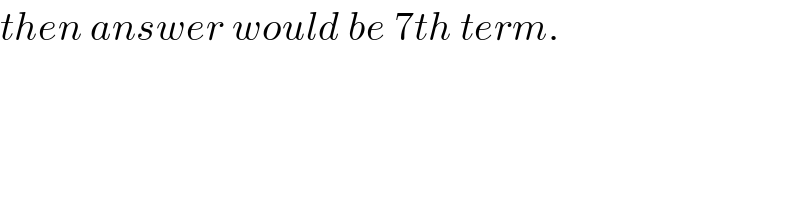
$${then}\:{answer}\:{would}\:{be}\:\mathrm{7}{th}\:{term}. \\ $$
Commented by Rio Michael last updated on 03/Oct/19

$${thanks}\:{guys} \\ $$
Commented by Rio Michael last updated on 03/Oct/19
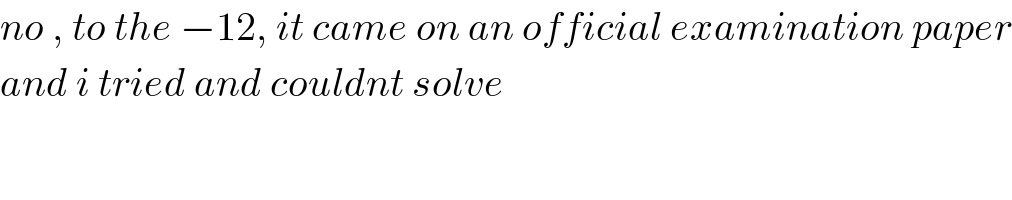
$${no}\:,\:{to}\:{the}\:−\mathrm{12},\:{it}\:{came}\:{on}\:{an}\:{official}\:{examination}\:{paper} \\ $$$${and}\:{i}\:{tried}\:{and}\:{couldnt}\:{solve} \\ $$
Answered by MJS last updated on 03/Oct/19
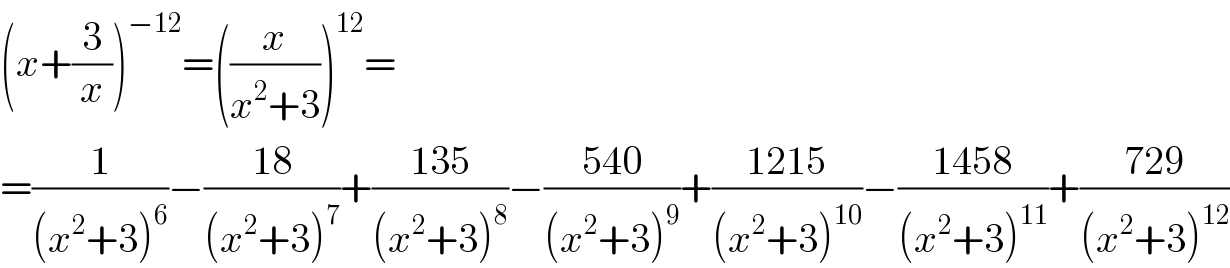
$$\left({x}+\frac{\mathrm{3}}{{x}}\right)^{−\mathrm{12}} =\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\mathrm{12}} = \\ $$$$=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{6}} }−\frac{\mathrm{18}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{7}} }+\frac{\mathrm{135}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{8}} }−\frac{\mathrm{540}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{9}} }+\frac{\mathrm{1215}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{10}} }−\frac{\mathrm{1458}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{11}} }+\frac{\mathrm{729}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{12}} } \\ $$
