Question Number 141814 by gsk2684 last updated on 12/Jul/21
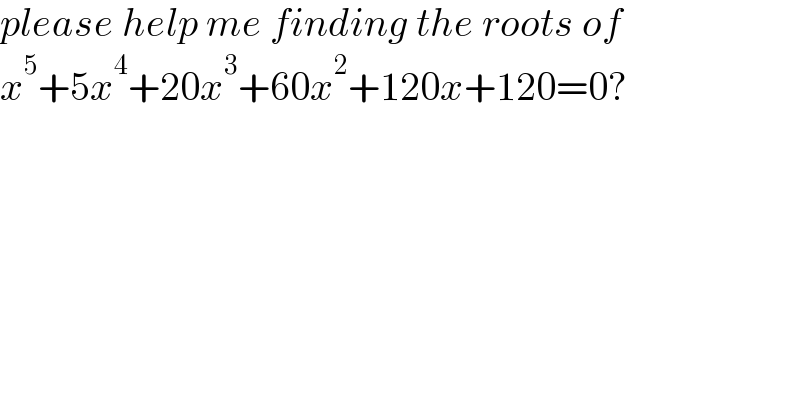
$${please}\:{help}\:{me}\:{finding}\:{the}\:{roots}\:{of}\:\: \\ $$$${x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} +\mathrm{20}{x}^{\mathrm{3}} +\mathrm{60}{x}^{\mathrm{2}} +\mathrm{120}{x}+\mathrm{120}=\mathrm{0}? \\ $$
Commented by MJS_new last updated on 23/May/21
$$\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{believe}\:\mathrm{me}? \\ $$
Commented by gsk2684 last updated on 23/May/21

$${Dear}\:{MJS},\:{I}\:{have}\:{registered} \\ $$$$\:{newly}\:{on}\:{this}\:{platform}.\:{I}\:{had}\:{belief}\: \\ $$$${on}\:{you}\:.\:{please}\:{help}\:{me}\:{in}\:{solving} \\ $$$${the}\:{problem}\:{to}\:{find}\:{the}\:{nature}\:{of}\: \\ $$$${roots}\:{and}\:{trace}\:{of}\:{the}\:{curve}. \\ $$
Answered by MJS_new last updated on 23/May/21

$${f}\left({x}\right)={x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} +\mathrm{20}{x}^{\mathrm{3}} +\mathrm{60}{x}^{\mathrm{2}} +\mathrm{120}{x}+\mathrm{120} \\ $$$$ \\ $$$${f}\:'\left({x}\right)=\mathrm{5}{x}^{\mathrm{4}} +\mathrm{20}{x}^{\mathrm{3}} +\mathrm{60}{x}^{\mathrm{2}} +\mathrm{120}{x}+\mathrm{120} \\ $$$${f}\:''\left({x}\right)=\mathrm{20}{x}^{\mathrm{3}} +\mathrm{60}{x}^{\mathrm{2}} +\mathrm{120}{x}+\mathrm{120} \\ $$$${f}\:''\left({x}\right)=\mathrm{0}\:\Rightarrow\:{x}\approx−\mathrm{1}.\mathrm{59607} \\ $$$${f}\:'\left(\approx−\mathrm{1}.\mathrm{59607}\right)\approx\mathrm{32}.\mathrm{4474}\:\Rightarrow\:{f}\:'\left({x}\right)>\mathrm{0}\:\forall{x}\in\mathbb{R}\:\Rightarrow \\ $$$$\Rightarrow\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{increasing}\:\forall{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{it}\:\mathrm{has}\:\mathrm{exactly} \\ $$$$\mathrm{one}\:\mathrm{real}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{first}\:\mathrm{we}\:\mathrm{try}\:\mathrm{all}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{constant}: \\ $$$$\pm\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},\:\mathrm{8},\:\mathrm{10},\:\mathrm{12},\:\mathrm{15},\:\mathrm{20},\:\mathrm{30},\:\mathrm{40},\:\mathrm{60},\:\mathrm{120}\right\} \\ $$$$\Rightarrow\:\mathrm{none}\:\mathrm{of}\:\mathrm{these}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{polynomes} \\ $$$$\mathrm{of}\:\mathrm{degree}\:\mathrm{5}\:\mathrm{or}\:\mathrm{higher}\:\Rightarrow\:\mathrm{we}\:\mathrm{must}\:\mathrm{approximate} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{120}\wedge{f}\left({x}\right)\:\mathrm{increasing}\:\Rightarrow\:\mathrm{search}\:<\mathrm{0} \\ $$$${f}\left(−\mathrm{1}\right)=\mathrm{44} \\ $$$${f}\left(−\mathrm{2}\right)=\mathrm{8} \\ $$$${f}\left(−\mathrm{3}\right)=−\mathrm{78} \\ $$$${f}\left(−\mathrm{2}.\mathrm{1}\right)=\mathrm{3}.\mathrm{77}… \\ $$$${f}\left(−\mathrm{2}.\mathrm{2}\right)=−.\mathrm{968}… \\ $$$${f}\left(−\mathrm{2}.\mathrm{19}\right)=−.\mathrm{465}… \\ $$$${f}\left(−\mathrm{2}.\mathrm{18}\right)=.\mathrm{0299}… \\ $$$$… \\ $$$$\Rightarrow\:{x}\approx−\mathrm{2}.\mathrm{18060712404} \\ $$
Commented by gsk2684 last updated on 24/May/21
$${thank}\:{you}\:{very}\:{much} \\ $$
