Question Number 140194 by mnjuly1970 last updated on 05/May/21
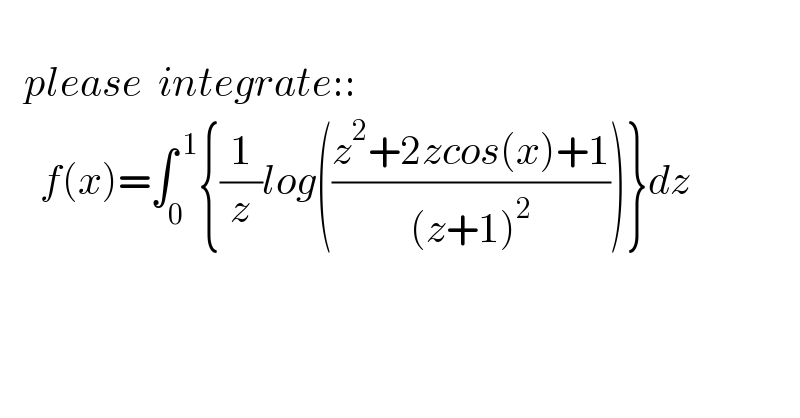
$$\:\: \\ $$$$\:\:\:{please}\:\:{integrate}:: \\ $$$$\:\:\:\:\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\frac{\mathrm{1}}{{z}}{log}\left(\frac{{z}^{\mathrm{2}} +\mathrm{2}{zcos}\left({x}\right)+\mathrm{1}}{\left({z}+\mathrm{1}\right)^{\mathrm{2}} }\right)\right\}{dz} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 05/May/21
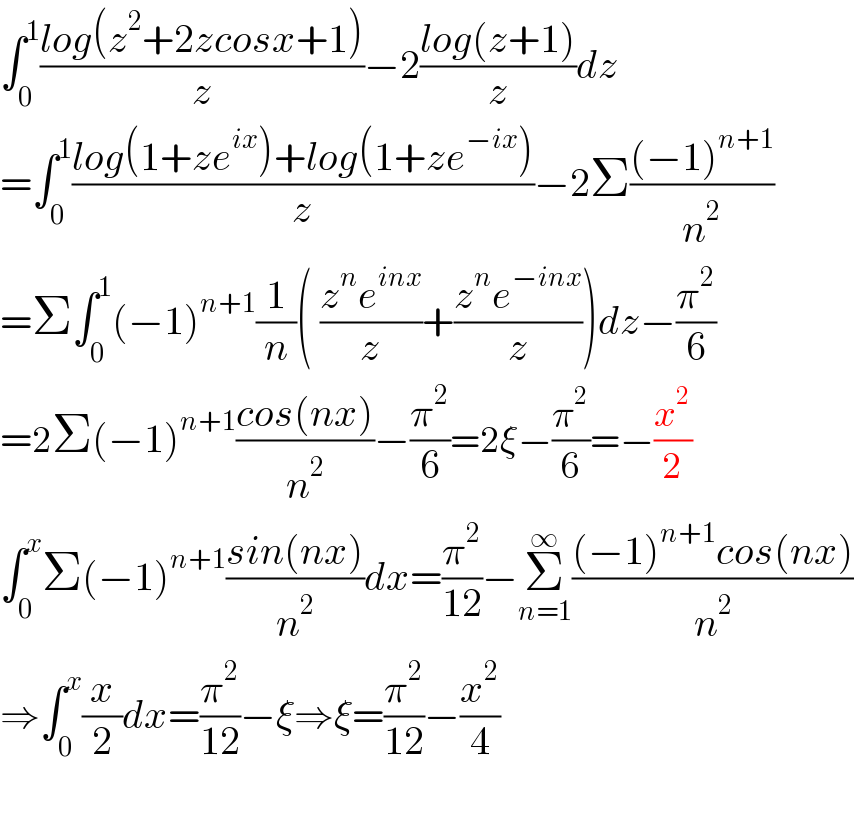
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({z}^{\mathrm{2}} +\mathrm{2}{zcosx}+\mathrm{1}\right)}{{z}}−\mathrm{2}\frac{{log}\left({z}+\mathrm{1}\right)}{{z}}{dz} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{ze}^{{ix}} \right)+{log}\left(\mathrm{1}+{ze}^{−{ix}} \right)}{{z}}−\mathrm{2}\Sigma\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} } \\ $$$$=\Sigma\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}}\left(\:\frac{{z}^{{n}} {e}^{{inx}} }{{z}}+\frac{{z}^{{n}} {e}^{−{inx}} }{{z}}\right){dz}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\mathrm{2}\Sigma\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\mathrm{2}\xi−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{{x}} \Sigma\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{{sin}\left({nx}\right)}{{n}^{\mathrm{2}} }{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {cos}\left({nx}\right)}{{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{{x}} \frac{{x}}{\mathrm{2}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\xi\Rightarrow\xi=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 05/May/21

$${perfect}\:{and}\:{nice}\:{solution} \\ $$$${thank}\:{you}… \\ $$
