Please-show-me-an-approach-to-solve-this-2-x-4x-Find-the-value-of-x-

Question Number 5734 by sanusihammed last updated on 25/May/16

$${Please}\:{show}\:{me}\:{an}\:{approach}\:{to}\:{solve}\:{this}… \\ $$$$ \\ $$$$\mathrm{2}^{{x}} \:=\:\mathrm{4}{x} \\ $$$$ \\ $$$${Find}\:{the}\:{value}\:{of}\:{x}\: \\ $$

Answered by prakash jain last updated on 25/May/16

2^x =4x 1=((4x)/2^x ) 1=((4x)/e^(xln 2) )=4xe^(−xln 2) (1/4)=xe^(−xln 2) ((−ln 2)/4)=−xln 2e^(−xln 2) W(−((ln 2)/4))=−xln 2 x=−((W(−((ln 2)/4)))/(ln 2)) W is product logarithm function W(xe^x )=x So W(−xln 2e^(−xln 2) )=−xln 2

$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$$$\mathrm{1}=\frac{\mathrm{4}{x}}{\mathrm{2}^{{x}} } \\ $$$$\mathrm{1}=\frac{\mathrm{4}{x}}{{e}^{{x}\mathrm{ln}\:\mathrm{2}} }=\mathrm{4}{xe}^{−{x}\mathrm{ln}\:\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}={xe}^{−{x}\mathrm{ln}\:\mathrm{2}} \\ $$$$\frac{−\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}=−{x}\mathrm{ln}\:\mathrm{2}{e}^{−{x}\mathrm{ln}\:\mathrm{2}} \\ $$$${W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)=−{x}\mathrm{ln}\:\mathrm{2} \\ $$$${x}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)}{\mathrm{ln}\:\mathrm{2}} \\ $$$${W}\:\mathrm{is}\:\mathrm{product}\:\mathrm{logarithm}\:\mathrm{function} \\ $$$${W}\left({xe}^{{x}} \right)={x}\: \\ $$$${S}\mathrm{o}\:{W}\left(−{x}\mathrm{ln}\:\mathrm{2}{e}^{−{x}\mathrm{ln}\:\mathrm{2}} \right)=−{x}\mathrm{ln}\:\mathrm{2} \\ $$

Commented by Yozzii last updated on 26/May/16

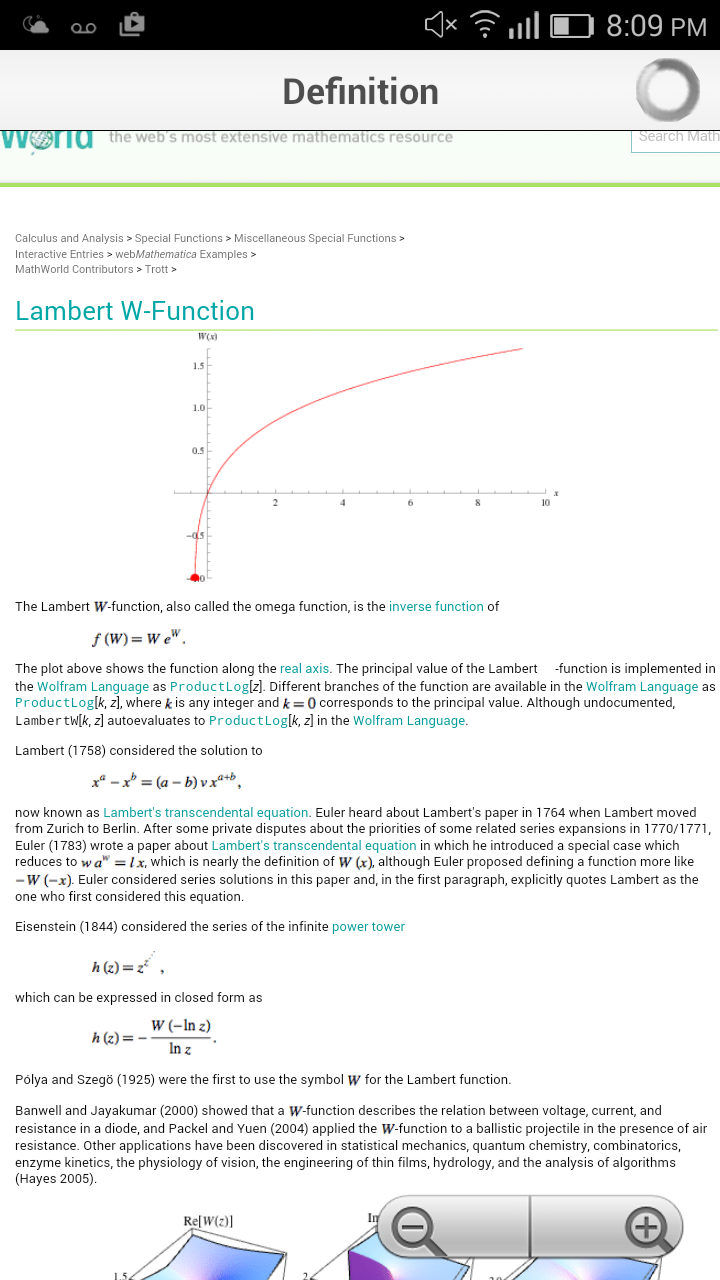
Commented by Yozzii last updated on 26/May/16

$${In}\:{case}\:{you}\:{wanted}\:{a}\:{bit}\:{more} \\ $$$${information}\:{on}\:{W}. \\ $$

Commented by Rasheed Soomro last updated on 26/May/16

How you derived ((−ln 2)/4)=−xln 2e^(−xln 2) from (1/4)=xe^(−xln 2) ? Please insert some steps more.

$${How}\:{you}\:{derived}\:\frac{−\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}=−{x}\mathrm{ln}\:\mathrm{2}{e}^{−{x}\mathrm{ln}\:\mathrm{2}} \\ $$$${from}\:\frac{\mathrm{1}}{\mathrm{4}}={xe}^{−{x}\mathrm{ln}\:\mathrm{2}} \:? \\ $$$${Please}\:{insert}\:{some}\:{steps}\:{more}. \\ $$

Commented by prakash jain last updated on 26/May/16

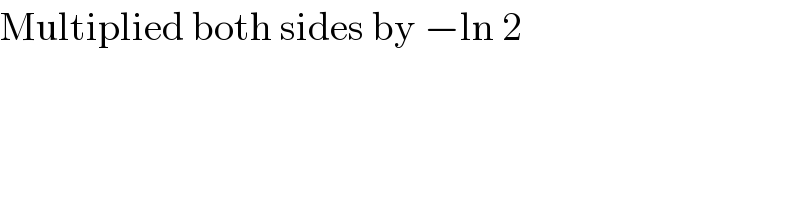
$$\mathrm{Multiplied}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:−\mathrm{ln}\:\mathrm{2} \\ $$

Commented by Rasheed Soomro last updated on 26/May/16

ThankS! I considered −xln 2e^(−xln 2) as −xln (2e^(−xln 2) ).So couldn′t understand.

$$\mathcal{T}{hank}\mathcal{S}!\:{I}\:{considered}\:−{x}\mathrm{ln}\:\mathrm{2}{e}^{−{x}\mathrm{ln}\:\mathrm{2}} \\ $$$${as}\:−{x}\mathrm{ln}\:\left(\mathrm{2}{e}^{−{x}\mathrm{ln}\:\mathrm{2}} \right).{So}\:{couldn}'{t}\:{understand}. \\ $$

Facebook Tweet Pin

Please-show-me-an-approach-to-solve-this-2-x-4x-Find-the-value-of-x-

Leave a Reply Cancel reply