Question Number 8798 by javawithfish last updated on 28/Oct/16
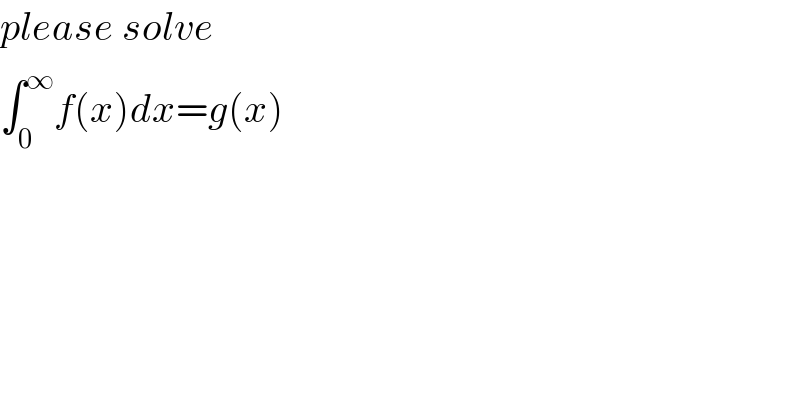
$${please}\:{solve} \\ $$$$\int_{\mathrm{0}} ^{\infty} {f}\left({x}\right){dx}={g}\left({x}\right) \\ $$
Commented by Yozzias last updated on 28/Oct/16
![Impossible unless g(x)=f(x)=0 ∀x∈R. The definite integral ∫_a ^b f(x)dx gives a real number iff f is integrable on [a,b]. We can say then that ∫_a ^( b) f(x)dx is a function h of the real variables a and b. ∴ h(a,b)=∫_a ^( b) f(x)dx (b≥a, (a,b)∈R^2 ) h cannot be a function of x therefore. Similarly ∫_0 ^( ∞) f(x)dx cannot be a function of x itself unless f(x)=0 ∀x∈R.](https://www.tinkutara.com/question/Q8799.png)
$$\mathrm{Impossible}\:\mathrm{unless}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\forall\mathrm{x}\in\mathbb{R}.\:\mathrm{The}\:\mathrm{definite}\: \\ $$$$\mathrm{integral}\:\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{gives}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number}\:\mathrm{iff}\:\mathrm{f}\:\mathrm{is} \\ $$$$\mathrm{integrable}\:\mathrm{on}\:\left[\mathrm{a},\mathrm{b}\right].\:\mathrm{We}\:\mathrm{can}\:\mathrm{say}\:\mathrm{then}\:\mathrm{that} \\ $$$$\int_{\mathrm{a}} ^{\:\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{is}\:\mathrm{a}\:\mathrm{function}\:\mathrm{h}\:\mathrm{of}\:\mathrm{the}\:\mathrm{real}\:\mathrm{variables} \\ $$$$\mathrm{a}\:\mathrm{and}\:\mathrm{b}.\:\therefore\:\mathrm{h}\left(\mathrm{a},\mathrm{b}\right)=\int_{\mathrm{a}} ^{\:\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:\left(\mathrm{b}\geqslant\mathrm{a},\:\left(\mathrm{a},\mathrm{b}\right)\in\mathbb{R}^{\mathrm{2}} \right) \\ $$$$\mathrm{h}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{x}\:\mathrm{therefore}.\:\mathrm{Similarly} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{x}\:\mathrm{itself} \\ $$$$\mathrm{unless}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0}\:\forall\mathrm{x}\in\mathbb{R}. \\ $$
Commented by javawithfish last updated on 28/Oct/16
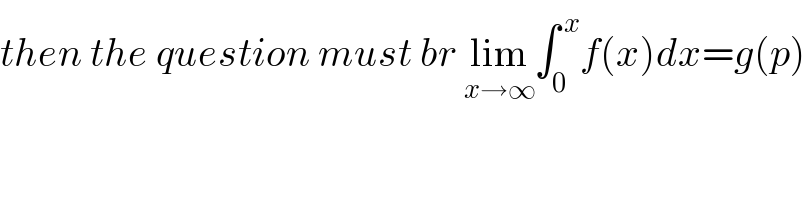
$${then}\:{the}\:{question}\:{must}\:{br}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\:{x}} {f}\left({x}\right){dx}={g}\left({p}\right) \\ $$
