Question Number 75701 by vishalbhardwaj last updated on 15/Dec/19
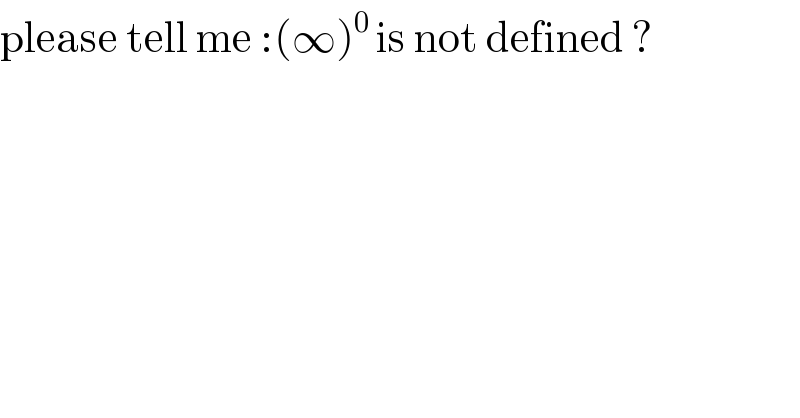
$$\mathrm{please}\:\mathrm{tell}\:\mathrm{me}\::\left(\infty\right)^{\mathrm{0}\:} \mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:? \\ $$
Commented by malwaan last updated on 16/Dec/19

$${yes} \\ $$$${but}\:\mathrm{0}^{\infty} \:=\:\mathrm{0} \\ $$
Answered by MJS last updated on 15/Dec/19

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{defined} \\ $$
Answered by aguy last updated on 15/Dec/19
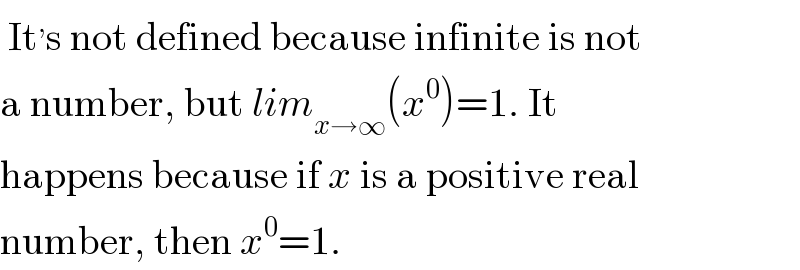
$$\:\mathrm{It}^{,} \mathrm{s}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{because}\:\mathrm{infinite}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{a}\:\mathrm{number},\:\mathrm{but}\:{lim}_{{x}\rightarrow\infty} \left({x}^{\mathrm{0}} \right)=\mathrm{1}.\:\mathrm{It} \\ $$$$\mathrm{happens}\:\mathrm{because}\:\mathrm{if}\:{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{real} \\ $$$$\mathrm{number},\:\mathrm{then}\:{x}^{\mathrm{0}} =\mathrm{1}. \\ $$
