Question Number 5153 by 1771727373 last updated on 23/Apr/16

$${proof}\:\:\:\:{e}^{{i}\Theta} ={cos}\left(\Theta\right)+{isin}\left(\Theta\right) \\ $$
Answered by 123456 last updated on 23/Apr/16
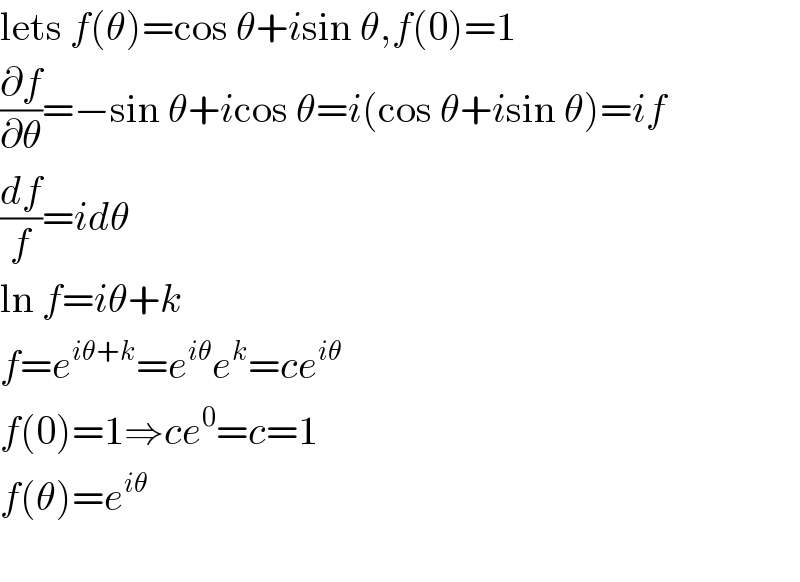
$$\mathrm{lets}\:{f}\left(\theta\right)=\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta,{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\frac{\partial{f}}{\partial\theta}=−\mathrm{sin}\:\theta+{i}\mathrm{cos}\:\theta={i}\left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right)={if} \\ $$$$\frac{{df}}{{f}}={id}\theta \\ $$$$\mathrm{ln}\:{f}={i}\theta+{k} \\ $$$${f}={e}^{{i}\theta+{k}} ={e}^{{i}\theta} {e}^{{k}} ={ce}^{{i}\theta} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1}\Rightarrow{ce}^{\mathrm{0}} ={c}=\mathrm{1} \\ $$$${f}\left(\theta\right)={e}^{{i}\theta} \\ $$$$ \\ $$
