Question Number 11549 by Nayon last updated on 28/Mar/17
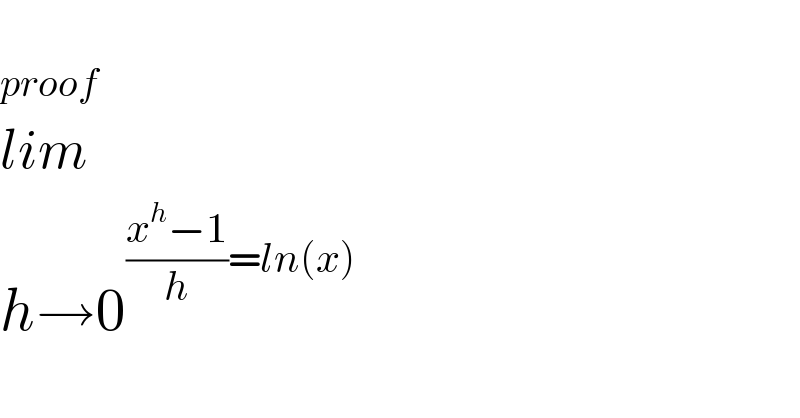
$$\:\:\:\: \\ $$$${proof} \\ $$$${lim} \\ $$$${h}\rightarrow\mathrm{0}^{\frac{{x}^{{h}} −\mathrm{1}}{{h}}={ln}\left({x}\right)} \\ $$
Answered by mrW1 last updated on 28/Mar/17
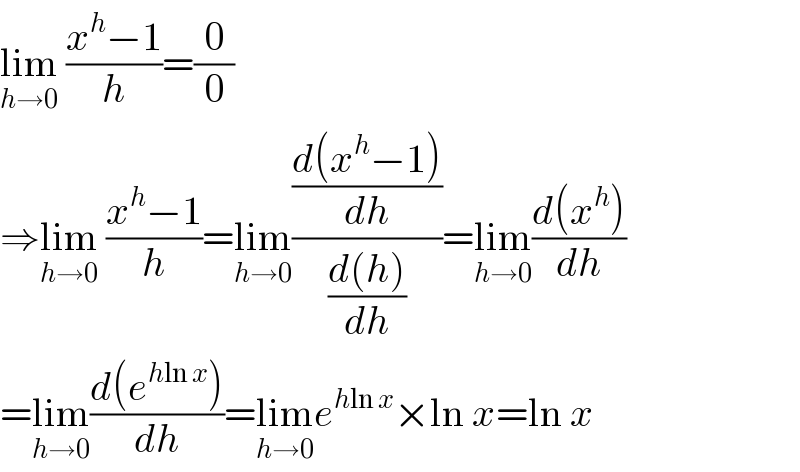
$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{{h}} −\mathrm{1}}{{h}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\Rightarrow\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{{h}} −\mathrm{1}}{{h}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}\left({x}^{{h}} −\mathrm{1}\right)}{{dh}}}{\frac{{d}\left({h}\right)}{{dh}}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{d}\left({x}^{{h}} \right)}{{dh}} \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{d}\left({e}^{{h}\mathrm{ln}\:{x}} \right)}{{dh}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}{e}^{{h}\mathrm{ln}\:{x}} ×\mathrm{ln}\:{x}=\mathrm{ln}\:{x} \\ $$
Commented by Nayon last updated on 28/Mar/17
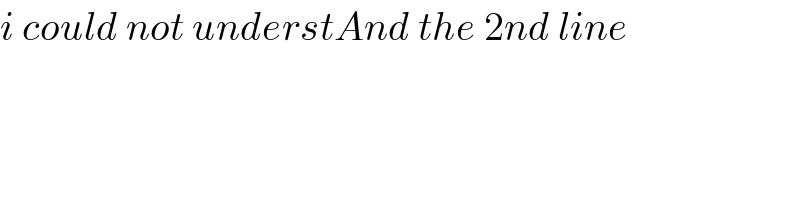
$${i}\:{could}\:{not}\:{understAnd}\:{the}\:\mathrm{2}{nd}\:{line} \\ $$
Commented by mrW1 last updated on 28/Mar/17
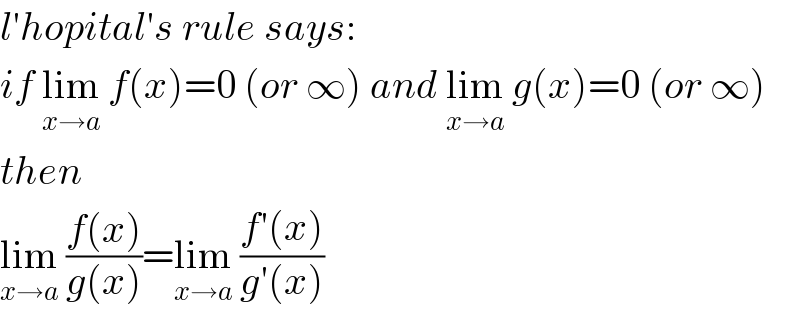
$${l}'{hopital}'{s}\:{rule}\:{says}: \\ $$$${if}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0}\:\left({or}\:\infty\right)\:{and}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{g}\left({x}\right)=\mathrm{0}\:\left({or}\:\infty\right) \\ $$$${then} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)} \\ $$
