Question Number 471 by 123456 last updated on 25/Jan/15
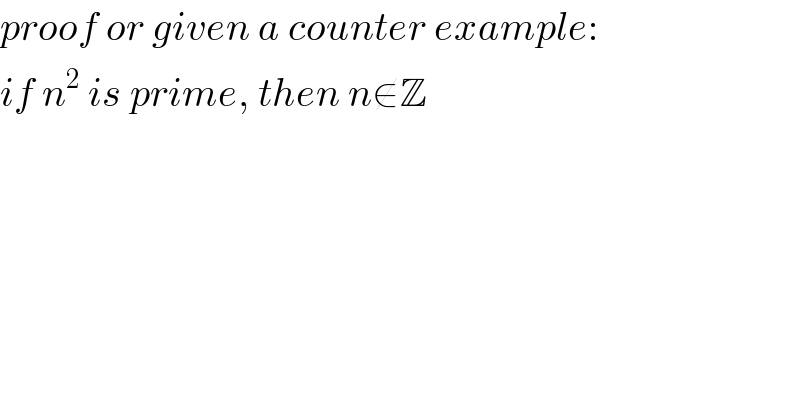
$${proof}\:{or}\:{given}\:{a}\:{counter}\:{example}: \\ $$$${if}\:{n}^{\mathrm{2}} \:{is}\:{prime},\:{then}\:{n}\notin\mathbb{Z} \\ $$
Answered by prakash jain last updated on 10/Jan/15
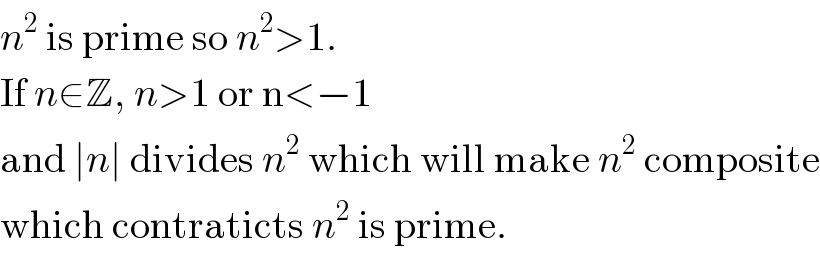
$${n}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{prime}\:\mathrm{so}\:{n}^{\mathrm{2}} >\mathrm{1}.\: \\ $$$$\mathrm{If}\:{n}\in\mathbb{Z},\:{n}>\mathrm{1}\:\mathrm{or}\:\mathrm{n}<−\mathrm{1} \\ $$$$\mathrm{and}\:\mid{n}\mid\:\mathrm{divides}\:{n}^{\mathrm{2}} \:\mathrm{which}\:\mathrm{will}\:\mathrm{make}\:{n}^{\mathrm{2}} \:\mathrm{composite} \\ $$$$\mathrm{which}\:\mathrm{contraticts}\:{n}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{prime}.\: \\ $$
