Question Number 143384 by mathdanisur last updated on 13/Jun/21
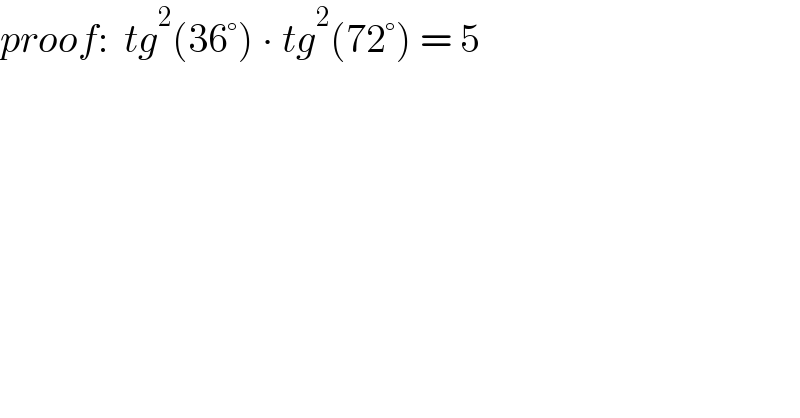
$${proof}:\:\:{tg}^{\mathrm{2}} \left(\mathrm{36}°\right)\:\centerdot\:{tg}^{\mathrm{2}} \left(\mathrm{72}°\right)\:=\:\mathrm{5} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Jun/21
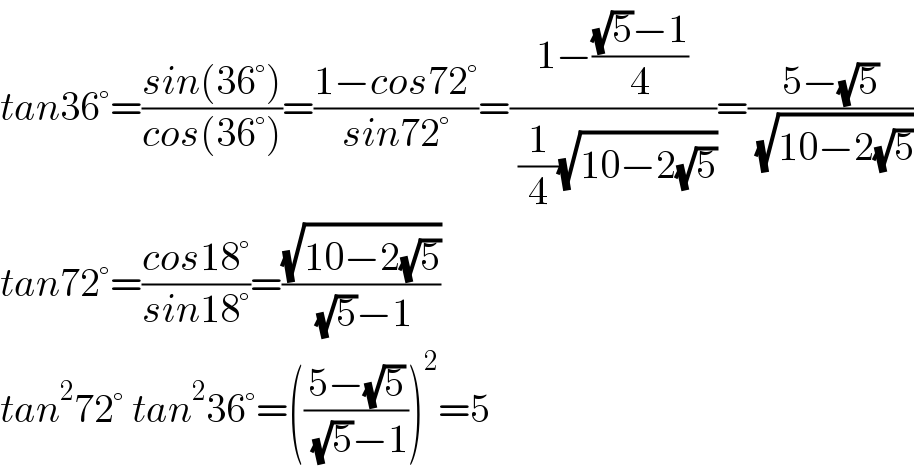
$${tan}\mathrm{36}°=\frac{{sin}\left(\mathrm{36}°\right)}{{cos}\left(\mathrm{36}°\right)}=\frac{\mathrm{1}−{cos}\mathrm{72}°}{{sin}\mathrm{72}°}=\frac{\mathrm{1}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}}{\:\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}=\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}} \\ $$$${tan}\mathrm{72}°=\frac{{cos}\mathrm{18}°}{{sin}\mathrm{18}°}=\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{5}}−\mathrm{1}} \\ $$$${tan}^{\mathrm{2}} \mathrm{72}°\:{tan}^{\mathrm{2}} \mathrm{36}°=\left(\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{5} \\ $$
Commented by mathdanisur last updated on 14/Jun/21

$${Sir}\:{thank}\:{you} \\ $$
Answered by Ar Brandon last updated on 13/Jun/21
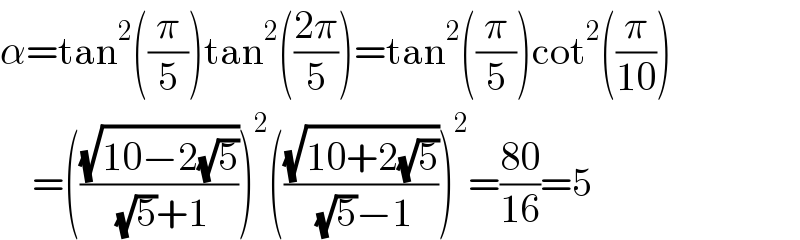
$$\alpha=\mathrm{tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)\mathrm{tan}^{\mathrm{2}} \left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right)=\mathrm{tan}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)\mathrm{cot}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right) \\ $$$$\:\:\:\:=\left(\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}\right)^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}\right)^{\mathrm{2}} =\frac{\mathrm{80}}{\mathrm{16}}=\mathrm{5} \\ $$
Commented by mathdanisur last updated on 14/Jun/21

$${thank}\:{you}\:{Sir} \\ $$
