Question Number 1694 by 123456 last updated on 01/Sep/15

$$\mathrm{proof}\:\mathrm{that}\:\mathrm{for}\:\mathrm{two}\:\mathrm{set}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\left(\mathrm{or}\:\mathrm{give}\:\mathrm{a}\:\mathrm{counter}\:\mathrm{example}\right) \\ $$$$\mid\mathrm{A}\cup\mathrm{B}\mid\geqslant\mid\mathrm{A}\cap\mathrm{B}\mid \\ $$
Answered by Rasheed Soomro last updated on 01/Sep/15
![In the following A and B are assumed as finite sets. A∩B ⊆A⊆ A∪B⇒∣A∩B∣≤∣A∣≤∣A∪B∣...........I A∩B ⊆B⊆ A∪B⇒∣A∩B∣≤∣B∣≤∣A∪B∣...........II From I and II on adding, 2∣A∩B∣≤∣A∣+∣B∣≤2∣A∪B∣ ∣A∩B∣≤((∣A∣+∣B∣)/2) ≤∣A∪B∣ [ Dividing by 2] ∣A∪B∣≥∣A∩B∣](https://www.tinkutara.com/question/Q1701.png)
$$\:\mathrm{In}\:\mathrm{the}\:\mathrm{following}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\boldsymbol{\mathrm{B}}\:\mathrm{are}\:\mathrm{assumed}\:\mathrm{as}\:\mathrm{finite}\:\mathrm{sets}. \\ $$$$\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\boldsymbol{\mathrm{A}}\subseteq\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid………..\boldsymbol{\mathrm{I}} \\ $$$$\:\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\boldsymbol{\mathrm{B}}\subseteq\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid………..\boldsymbol{\mathrm{II}} \\ $$$$\:\mathrm{From}\:\boldsymbol{\mathrm{I}}\:\mathrm{and}\:\boldsymbol{\mathrm{II}}\:\mathrm{on}\:\mathrm{adding}, \\ $$$$\:\mathrm{2}\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid\leqslant\mathrm{2}\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid \\ $$$$\:\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\frac{\mid\boldsymbol{\mathrm{A}}\mid+\mid\boldsymbol{\mathrm{B}}\mid}{\mathrm{2}}\:\leqslant\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\:\:\:\:\left[\:\mathrm{Dividing}\:\mathrm{by}\:\mathrm{2}\right] \\ $$$$\:\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\geqslant\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid \\ $$
Answered by Rasheed Soomro last updated on 01/Sep/15
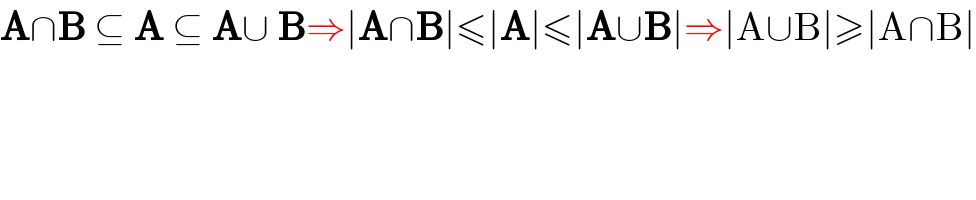
$$\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\subseteq\:\boldsymbol{\mathrm{A}}\:\subseteq\:\boldsymbol{\mathrm{A}}\cup\:\boldsymbol{\mathrm{B}}\Rightarrow\mid\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\mid\leqslant\mid\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}\mid\Rightarrow\mid\mathrm{A}\cup\mathrm{B}\mid\geqslant\mid\mathrm{A}\cap\mathrm{B}\mid \\ $$
