Question Number 658 by 123456 last updated on 22/Feb/15
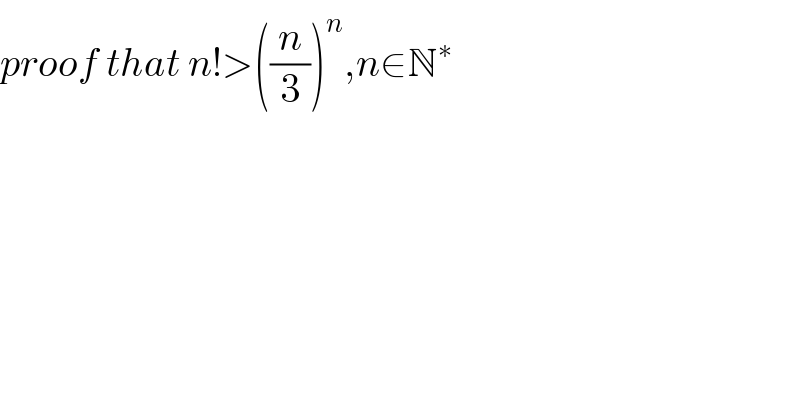
$${proof}\:{that}\:{n}!>\left(\frac{{n}}{\mathrm{3}}\right)^{{n}} ,{n}\in\mathbb{N}^{\ast} \\ $$
Commented by 123456 last updated on 20/Feb/15
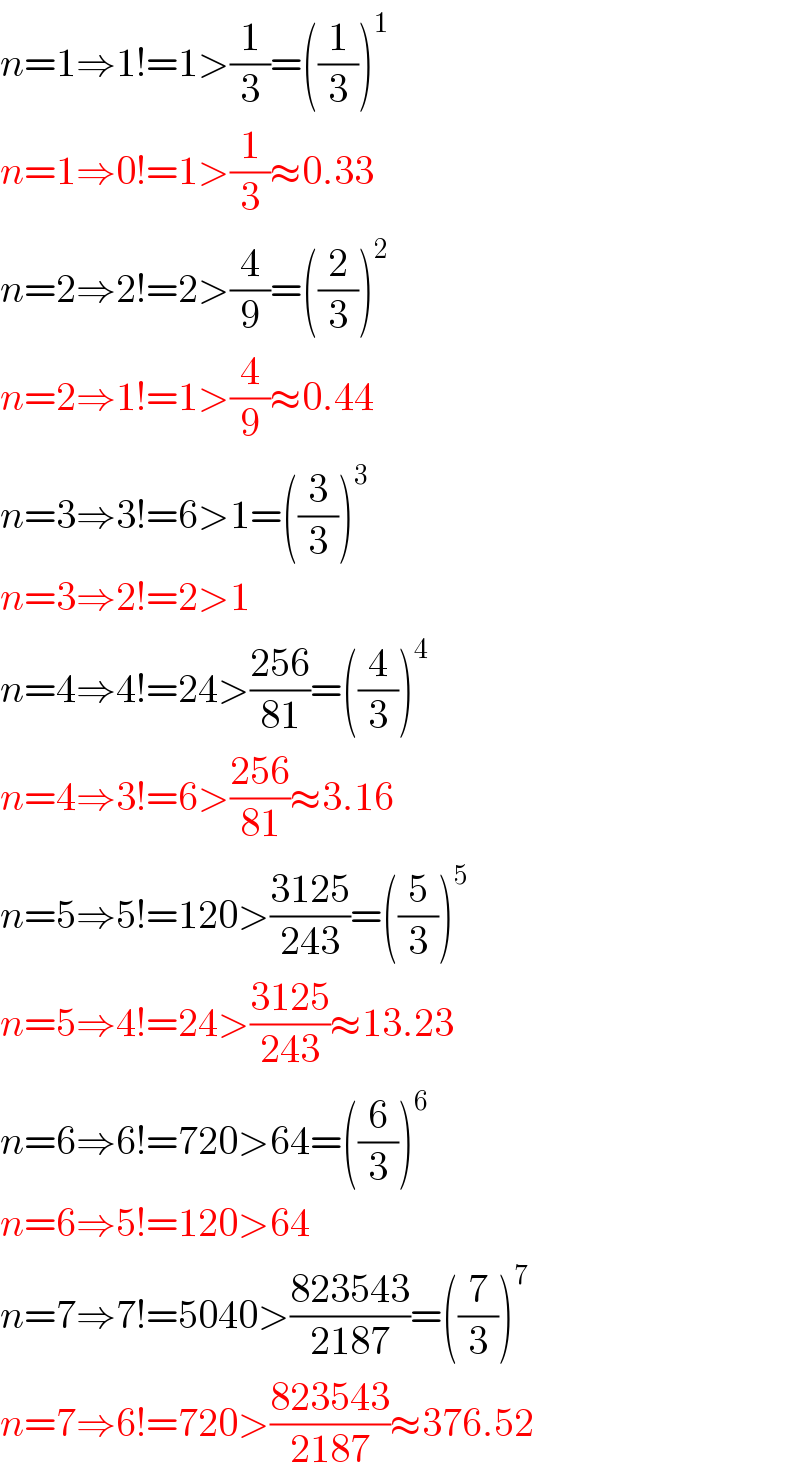
$${n}=\mathrm{1}\Rightarrow\mathrm{1}!=\mathrm{1}>\frac{\mathrm{1}}{\mathrm{3}}=\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{1}} \\ $$$${n}=\mathrm{1}\Rightarrow\mathrm{0}!=\mathrm{1}>\frac{\mathrm{1}}{\mathrm{3}}\approx\mathrm{0}.\mathrm{33} \\ $$$${n}=\mathrm{2}\Rightarrow\mathrm{2}!=\mathrm{2}>\frac{\mathrm{4}}{\mathrm{9}}=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${n}=\mathrm{2}\Rightarrow\mathrm{1}!=\mathrm{1}>\frac{\mathrm{4}}{\mathrm{9}}\approx\mathrm{0}.\mathrm{44} \\ $$$${n}=\mathrm{3}\Rightarrow\mathrm{3}!=\mathrm{6}>\mathrm{1}=\left(\frac{\mathrm{3}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$${n}=\mathrm{3}\Rightarrow\mathrm{2}!=\mathrm{2}>\mathrm{1} \\ $$$${n}=\mathrm{4}\Rightarrow\mathrm{4}!=\mathrm{24}>\frac{\mathrm{256}}{\mathrm{81}}=\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{4}} \\ $$$${n}=\mathrm{4}\Rightarrow\mathrm{3}!=\mathrm{6}>\frac{\mathrm{256}}{\mathrm{81}}\approx\mathrm{3}.\mathrm{16} \\ $$$${n}=\mathrm{5}\Rightarrow\mathrm{5}!=\mathrm{120}>\frac{\mathrm{3125}}{\mathrm{243}}=\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{5}} \\ $$$${n}=\mathrm{5}\Rightarrow\mathrm{4}!=\mathrm{24}>\frac{\mathrm{3125}}{\mathrm{243}}\approx\mathrm{13}.\mathrm{23} \\ $$$${n}=\mathrm{6}\Rightarrow\mathrm{6}!=\mathrm{720}>\mathrm{64}=\left(\frac{\mathrm{6}}{\mathrm{3}}\right)^{\mathrm{6}} \\ $$$${n}=\mathrm{6}\Rightarrow\mathrm{5}!=\mathrm{120}>\mathrm{64} \\ $$$${n}=\mathrm{7}\Rightarrow\mathrm{7}!=\mathrm{5040}>\frac{\mathrm{823543}}{\mathrm{2187}}=\left(\frac{\mathrm{7}}{\mathrm{3}}\right)^{\mathrm{7}} \\ $$$${n}=\mathrm{7}\Rightarrow\mathrm{6}!=\mathrm{720}>\frac{\mathrm{823543}}{\mathrm{2187}}\approx\mathrm{376}.\mathrm{52} \\ $$
Commented by 123456 last updated on 20/Feb/15
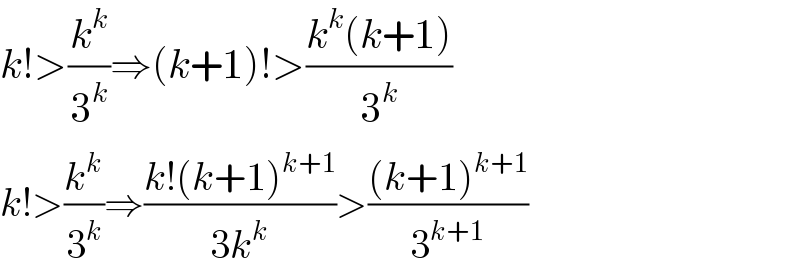
$${k}!>\frac{{k}^{{k}} }{\mathrm{3}^{{k}} }\Rightarrow\left({k}+\mathrm{1}\right)!>\frac{{k}^{{k}} \left({k}+\mathrm{1}\right)}{\mathrm{3}^{{k}} } \\ $$$${k}!>\frac{{k}^{{k}} }{\mathrm{3}^{{k}} }\Rightarrow\frac{{k}!\left({k}+\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{3}{k}^{{k}} }>\frac{\left({k}+\mathrm{1}\right)^{{k}+\mathrm{1}} }{\mathrm{3}^{{k}+\mathrm{1}} } \\ $$
